| 释义 |
p-GroupA Finite Group of Order  for for 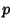 a Prime is called a a Prime is called a 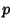 -group. Sylow provedthat every Group of this form has a Power-commutator representation on -group. Sylow provedthat every Group of this form has a Power-commutator representation on 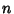 generators defined by generators defined by
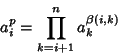 | (1) |
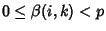 , ,  and and
 | (2) |
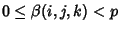 , ,  . If . If 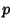 is Prime and is Prime and 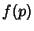 the number of Groups of order the number of Groups of order 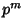 , then , then
 | (3) |
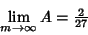 | (4) |
References
Higman, G. ``Enumerating 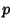 -Groups. I. Inequalities.'' Proc. London Math. Soc. 10, 24-30, 1960a. -Groups. I. Inequalities.'' Proc. London Math. Soc. 10, 24-30, 1960a.Higman, G. ``Enumerating 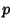 -Groups. II. Problems Whose Solution is PORC.'' Proc. London Math. Soc. 10, 566-582, 1960b. -Groups. II. Problems Whose Solution is PORC.'' Proc. London Math. Soc. 10, 566-582, 1960b.
|
![]() for
for ![]() a Prime is called a
a Prime is called a ![]() -group. Sylow provedthat every Group of this form has a Power-commutator representation on
-group. Sylow provedthat every Group of this form has a Power-commutator representation on ![]() generators defined by
generators defined by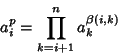

![]() -Groups. I. Inequalities.'' Proc. London Math. Soc. 10, 24-30, 1960a.
-Groups. I. Inequalities.'' Proc. London Math. Soc. 10, 24-30, 1960a.![]() -Groups. II. Problems Whose Solution is PORC.'' Proc. London Math. Soc. 10, 566-582, 1960b.
-Groups. II. Problems Whose Solution is PORC.'' Proc. London Math. Soc. 10, 566-582, 1960b.