| 释义 |
Euler-Mascheroni ConstantThe Euler-Mascheroni constant is denoted  (or sometimes (or sometimes  ) and has the numerical value ) and has the numerical value
 | (1) |
It is not known if this constant is Irrational, let alone Transcendental. However, Conway and Guy (1996) are ``prepared to bet that it is transcendental,'' althoughthey do not expect a proof to be achieved within their lifetimes.
The Euler-Mascheroni constant arises in many integrals
and sums
where  is the Riemann Zeta Function and is the Riemann Zeta Function and  are the Bernoulli Numbers. It is also given by the Euler Product are the Bernoulli Numbers. It is also given by the Euler Product
 | (10) |
 . Another connection with the Primes was provided byDirichlet's . Another connection with the Primes was provided byDirichlet's  1838 proof that the average number of Divisors of all numbers from 1 to 1838 proof that the average number of Divisors of all numbers from 1 to is asymptotic to is asymptotic to
 | (11) |
 is divided by all Primes is divided by all Primes , then the average amount by which the Quotient is less than the next whole number is , then the average amount by which the Quotient is less than the next whole number is  . .
Infinite Products involving  also arise from the G-Functionwith Positive Integer also arise from the G-Functionwith Positive Integer  . The cases . The cases  and and  give give
The Euler-Mascheroni constant is also given by the limits
(Le Lionnais 1983).
The difference between the  th convergent in (6) and th convergent in (6) and  is given by is given by
 | (17) |
 is the Floor Function, and satisfies the Inequality is the Floor Function, and satisfies the Inequality
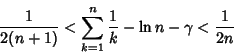 | (18) |
 | (19) |
 | (20) |
 | (21) |
 is a Binomial Coefficient (Beeler et al. 1972, Item 120, with is a Binomial Coefficient (Beeler et al. 1972, Item 120, with  replacing the undefined replacing the undefined  ). Bailey (1988) gives ). Bailey (1988) gives
 | (22) |
The symbol  is sometimes also used for is sometimes also used for
 | (23) |
Odena (1982-1983) gave the strange approximation
 | (24) |
No quadratically converging algorithm for computing  is known (Bailey 1988). 7,000,000 digits of is known (Bailey 1988). 7,000,000 digits of  have been computed as of Feb. 1998 (Plouffe). have been computed as of Feb. 1998 (Plouffe). See also Euler Product, Mertens Theorem, Stieltjes Constants
References
Bailey, D. H. ``Numerical Results on the Transcendence of Constants Involving  , , 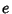 , and Euler's Constant.'' Math. Comput. 50, 275-281, 1988. , and Euler's Constant.'' Math. Comput. 50, 275-281, 1988.Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972. Brent, R. P. ``Computation of the Regular Continued Fraction for Euler's Constant.'' Math. Comput. 31, 771-777, 1977. Brent, R. P. and McMillan, E. M. ``Some New Algorithms for High-Precision Computation of Euler's Constant.'' Math. Comput. 34, 305-312, 1980. Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988. Conway, J. H. and Guy, R. K. ``The Euler-Mascheroni Number.'' In The Book of Numbers. New York: Springer-Verlag, pp. 260-261, 1996. de la Vallée Poussin, C.-J. Untitled communication. Annales de la Soc. Sci. Bruxelles 22, 84-90, 1898. DeTemple, D. W. ``A Quicker Convergence to Euler's Constant.'' Amer. Math. Monthly 100, 468-470, 1993. Dirichlet, G. L. J. für Math. 18, 273, 1838. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/euler/euler.html Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript, 1996. http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps. Gerst, I. ``Some Series for Euler's Constant.'' Amer. Math. Monthly 76, 273-275, 1969. Glaisher, J. W. L. ``On the History of Euler's Constant.'' Messenger of Math. 1, 25-30, 1872. Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA: Academic Press, 1979. Knuth, D. E. ``Euler's Constant to 1271 Places.'' Math. Comput. 16, 275-281, 1962. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 28, 1983. Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computationof Constants.'' http://www.lacim.uqam.ca/pi/records.html. Sloane, N. J. A. SequencesA033091,A033092,A033149,A046114,A046114,A001620/M3755, andA002852/M0097in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Sweeney, D. W. ``On the Computation of Euler's Constant.'' Math. Comput. 17, 170-178, 1963. Vacca, G. ``A New Series for the Eulerian Constant.'' Quart. J. Pure Appl. Math. 41, 363-368, 1910. Young, R. M. ``Euler's Constant.'' Math. Gaz. 75, 187-190, 1991. |
![]() (or sometimes
(or sometimes ![]() ) and has the numerical value
) and has the numerical value








![]() also arise from the G-Functionwith Positive Integer
also arise from the G-Functionwith Positive Integer ![]() . The cases
. The cases ![]() and
and ![]() give
give
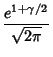


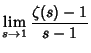

![]() th convergent in (6) and
th convergent in (6) and ![]() is given by
is given by
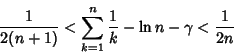




![]() is sometimes also used for
is sometimes also used for


![]() is known (Bailey 1988). 7,000,000 digits of
is known (Bailey 1988). 7,000,000 digits of ![]() have been computed as of Feb. 1998 (Plouffe).
have been computed as of Feb. 1998 (Plouffe).![]() ,
, ![]() , and Euler's Constant.'' Math. Comput. 50, 275-281, 1988.
, and Euler's Constant.'' Math. Comput. 50, 275-281, 1988.