| 释义 |
Euler SumIn response to a letter from Goldbach, Euler  considered Double Sums of the form considered Double Sums of the form
with 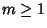 and and 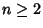 and where and where  is the Euler-Mascheroni Constant and is the Euler-Mascheroni Constant and 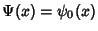 isthe Digamma Function. Euler found explicit formulas in terms of the Riemann Zeta Functionfor isthe Digamma Function. Euler found explicit formulas in terms of the Riemann Zeta Functionfor 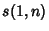 with with 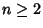 , and E. Au-Yeung numerically discovered , and E. Au-Yeung numerically discovered
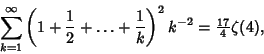 | (3) |
 is the Riemann Zeta Function, which was subsequently rigorously proven true (Borwein andBorwein 1995). Sums involving is the Riemann Zeta Function, which was subsequently rigorously proven true (Borwein andBorwein 1995). Sums involving  can be re-expressed in terms of sums the form can be re-expressed in terms of sums the form 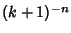 via and via and
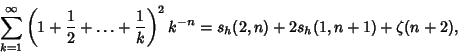 | (5) |
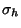 is defined below. is defined below.
Bailey et al. (1994) subsequently considered sums of the forms
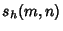 |  | 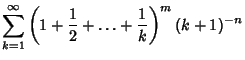 | (6) | 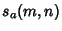 |  | 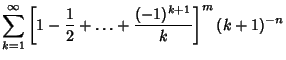 | (7) | 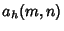 |  | 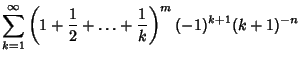 | (8) | 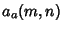 |  | 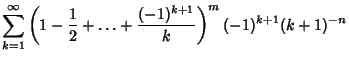 | | | | | | (9) | 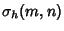 |  | 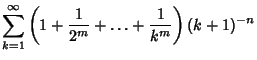 | (10) | 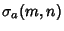 |  | 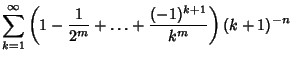 | (11) |  |  | 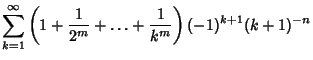 | (12) | | | | | (13) |  |  | 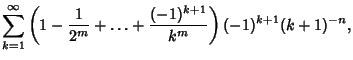 | | | | | | (14) |
where 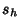 and and 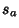 have the special forms have the special forms
Analytic single or double sums over  can be constructed for can be constructed for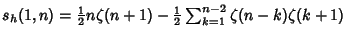 | (17) |  | | 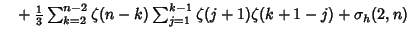 | (18) | 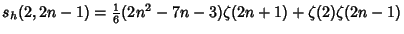 | | 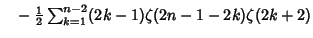 | |  | (19) | 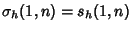 | (20) | 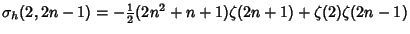 | | 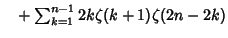 | (21) | 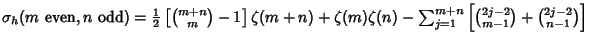 | | 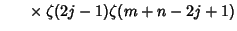 | (22) |  | | 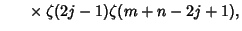 | (23) |
where 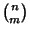 is a Binomial Coefficient. Explicit formulas inferred using the PSLQ Algorithm include is a Binomial Coefficient. Explicit formulas inferred using the PSLQ Algorithm include
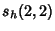 |  | 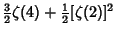 | (24) | | |  | 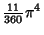 | (25) |  |  | 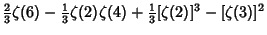 | (26) | | |  | 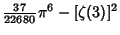 | (27) |  |  | 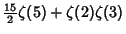 | (28) | 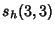 |  | 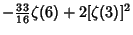 | (29) | 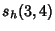 |  |  | (30) | 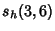 |  | 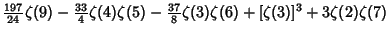 | (31) | 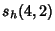 |  | 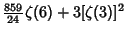 | (32) | 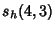 |  | 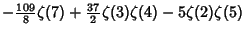 | (33) | 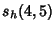 |  | 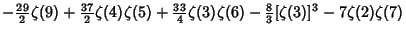 | (34) | 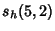 |  | 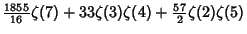 | (35) | 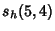 |  | 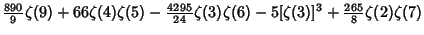 | (36) | 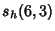 |  | 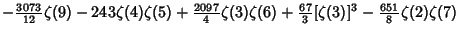 | (37) |  |  | 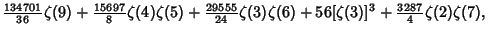 | (38) |
and
where  is a Polylogarithm, and is a Polylogarithm, and  is the Riemann Zeta Function (Bailey and Plouffe).Of these, only is the Riemann Zeta Function (Bailey and Plouffe).Of these, only 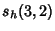 , , 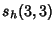 and the identities for and the identities for 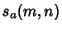 , ,  and and 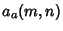 have been rigorouslyestablished. have been rigorouslyestablished.
References
Bailey, D. and Plouffe, S. ``Recognizing Numerical Constants.'' http://www.cecm.sfu.ca/organics/papers/bailey/.Bailey, D. H.; Borwein, J. M.; and Girgensohn, R. ``Experimental Evaluation of Euler Sums.'' Exper. Math. 3, 17-30, 1994. Berndt, B. C. Ramanujan's Notebooks: Part I. New York: Springer-Verlag, 1985. Borwein, D. and Borwein, J. M. ``On an Intriguing Integral and Some Series Related to 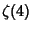 .'' Proc. Amer. Math. Soc. 123, 1191-1198, 1995. .'' Proc. Amer. Math. Soc. 123, 1191-1198, 1995. Borwein, D.; Borwein, J. M.; and Girgensohn, R. ``Explicit Evaluation of Euler Sums.'' Proc. Edinburgh Math. Soc. 38, 277-294, 1995. de Doelder, P. J. ``On Some Series Containing 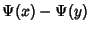 and and 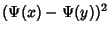 for Certain Values of for Certain Values of  and and 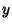 .'' J. Comp. Appl. Math. 37, 125-141, 1991. .'' J. Comp. Appl. Math. 37, 125-141, 1991. |
![]() considered Double Sums of the form
considered Double Sums of the form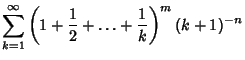
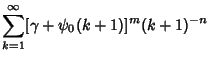
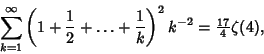
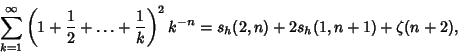
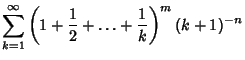
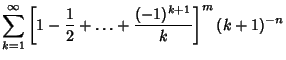
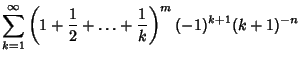
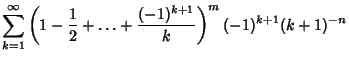
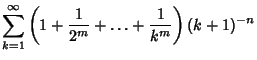
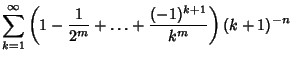
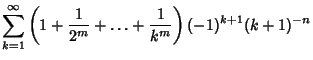
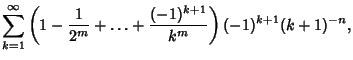
![]() and
and ![]() have the special forms
have the special forms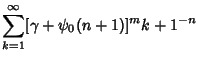
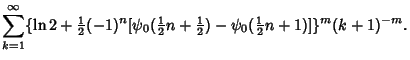
![]() is a Binomial Coefficient. Explicit formulas inferred using the PSLQ Algorithm include
is a Binomial Coefficient. Explicit formulas inferred using the PSLQ Algorithm include![]() .'' Proc. Amer. Math. Soc. 123, 1191-1198, 1995.
.'' Proc. Amer. Math. Soc. 123, 1191-1198, 1995.![]() and
and ![]() for Certain Values of
for Certain Values of ![]() and
and ![]() .'' J. Comp. Appl. Math. 37, 125-141, 1991.
.'' J. Comp. Appl. Math. 37, 125-141, 1991.