| 释义 |
Fibonacci n-Step NumberAn 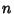 -step Fibonacci sequence is given by defining -step Fibonacci sequence is given by defining  for for  , , 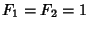 , ,  , and , and
 | (1) |
 . The case . The case  corresponds to the degenerate 1, 1, 2, 2, 2, 2 ..., corresponds to the degenerate 1, 1, 2, 2, 2, 2 ...,  to the usual FibonacciNumbers 1, 1, 2, 3, 5, 8, ... (Sloane's A000045), to the usual FibonacciNumbers 1, 1, 2, 3, 5, 8, ... (Sloane's A000045), 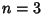 to the A000073), to the A000073),  to the Tetranacci Numbers1, 1, 2, 4, 8, 15, 29, 56, 108, ... (Sloane's A000078), etc. to the Tetranacci Numbers1, 1, 2, 4, 8, 15, 29, 56, 108, ... (Sloane's A000078), etc.
The limit  is given by solving is given by solving
 | (2) |
 and taking the Real Root and taking the Real Root  . If . If  , the equation reduces to , the equation reduces to
 | (3) |
 | (4) |
 | (5) |
 | (6) |
 , 2, ... are given numerically by 1, 1.61803, 1.83929, 1.92756, 1.96595, ..., approaching 2 as , 2, ... are given numerically by 1, 1.61803, 1.83929, 1.92756, 1.96595, ..., approaching 2 as .See also Fibonacci Number, Tribonacci Number .See also Fibonacci Number, Tribonacci Number
References
Sloane, N. J. A. SequencesA000045/M0692,A000073/M1074, andA000078/M1108in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
![]() -step Fibonacci sequence is given by defining
-step Fibonacci sequence is given by defining ![]() for
for ![]() ,
, ![]() ,
, ![]() , and
, and 
![]() is given by solving
is given by solving