“Finite Group Z2Z2”的概念、定义、习题解题方法及翻译-数学辞典

单词

Finite Group Z2Z2

释义

Finite Group Z2Z2

One of the two groups of Order 4. The name of this group derives from the fact that it is aDirect Product of two Subgroups. Like the group , is an Abelian Group. Unlike , however, it is not Cyclic. In addition tosatisfying for each element , it also satisfies , where 1 is the Identity Element. Examples of the group include the Viergruppe, Point Groups , , and , andthe Modulo Multiplication Groups and . That , the ResidueClasses prime to 8 given by , are a group of type can be shown by verifyingthat

(1)

and

(2)

is therefore a Modulo Multiplication Group.

The Cycle Graph is shown above, and the multiplication table for the group is given below.

	1
1	1
		1
			1
				1

The Conjugacy Classes are , ,

			(3)
			(4)
			(5)

			(6)
			(7)

and

Now explicitly consider the elements of the Point Group.

In terms of the Viergruppe elements

A reducible representation using 2-D Real Matrices is

			(8)
			(9)
			(10)
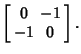			(11)

Another reducible representation using 3-D Real Matrices can be obtained from thesymmetry elements of the

group (1,

, and

) or

group (1,

, and

). Place the

axis along the

-axis,

in the

plane, and

in the

plane.

			(12)
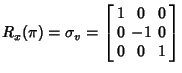			(13)
			(14)
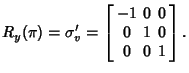			(15)

In order to find the irreducible representations, note that the traces are given by

and

Therefore, there are at least three distinct Conjugacy Classes. However, we see from the Multiplication Table that there are actually four ConjugacyClasses, so group rule 5 requires that there must be four irreducible representations. By rule 1, we arelooking for Positive Integers which satisfy

(16)

The only combination which will work is

(17)

so there are four one-dimensional representations. Rule 2 requires that the sum of the squares equal the Order

, so each 1-D representation must have Character

.Rule 6 requires that a totally symmetric representation always exists, so we are free to start off with the firstrepresentation having all 1s. We then use orthogonality (rule 3) to build up the other representations. The simplestsolution is then given by

1
1	1	1	1
1			1
1		1
1	1

These can be put into a more familiar form by switching and , giving the Character Table

1
1		1
1			1
1	1	1	1
1	1

The matrices corresponding to this representation are now

			(18)
			(19)
			(20)
			(21)

which consist of the previous representation with an additional component. These matrices are now orthogonal, and theorder equals the matrix dimension. As before,

See also Finite Group Z4

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。