Fractal Sequence
Given an Infinitive Sequence ![]() with associated array
with associated array ![]() , then
, then ![]() is said to be a fractal sequence
is said to be a fractal sequence
- 1. If
 , then there exists
, then there exists 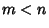 such that
such that 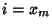 ,
, - 2. If
 , then, for every
, then, for every 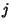 , there is exactly one
, there is exactly one 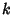 such that
such that 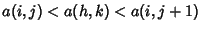 .
.
If ![]() is a fractal sequence, then the associated array is an Interspersion. If
is a fractal sequence, then the associated array is an Interspersion. If ![]() is a fractal sequence, thenthe Upper-Trimmed Subsequence is given by
is a fractal sequence, thenthe Upper-Trimmed Subsequence is given by ![]() , and the Lower-Trimmed Subsequence
, and the Lower-Trimmed Subsequence ![]() is anotherfractal sequence. The Signature of an Irrational Number is a fractal sequence.
is anotherfractal sequence. The Signature of an Irrational Number is a fractal sequence.
References
Kimberling, C. ``Fractal Sequences and Interspersions.'' Ars Combin. 45, 157-168, 1997.
- Proportional
- Proposition
- Propositional Calculus
- Prosthaphaeresis Formulas
- Proth's Theorem
- Protractor
- Prouhet's Problem
- Prussian Hat
- Prüfer Ring
- p-Series
- Pseudoanalytic Function
- Pseudocrosscap
- Pseudocylindrical Projection
- Pseudogroup
- Pseudolemniscate Case
- Pseudoperfect Number
- Pseudoprime
- Pseudorandom Number
- Pseudorhombicuboctahedron
- Pseudoscalar
- Pseudosmarandache Function
- Pseudosphere
- Pseudosquare
- Pseudotensor
- Pseudovector