| 释义 |
Kauffman Polynomial FA semi-oriented 2-variable Knot Polynomial defined by
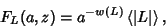 | (1) |
 is an oriented Link Diagram, is an oriented Link Diagram,  is the Writhe of is the Writhe of  , ,  is the unoriented diagramcorresponding to is the unoriented diagramcorresponding to  , and , and 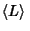 is the Bracket Polynomial. It was developed by Kauffman by extending the BLM/Ho Polynomial is the Bracket Polynomial. It was developed by Kauffman by extending the BLM/Ho Polynomial  to two variables, and satisfies to two variables, and satisfies
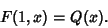 | (2) |
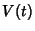 since it satisfies since it satisfies
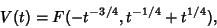 | (3) |
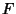 by a Power of by a Power of 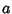 . In particular, suppose . In particular, suppose 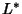 is obtained from is obtained from  by reversing the orientation of component by reversing the orientation of component  , then , then
 | (4) |
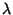 is the Linking Number of is the Linking Number of  with with 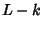 (Lickorish and Millett 1988). (Lickorish and Millett 1988). 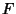 is unchanged by Mutation. is unchanged by Mutation.
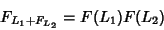 | (5) |
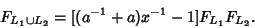 | (6) |
References
Lickorish, W. B. R. and Millett, B. R. ``The New Polynomial Invariants of Knots and Links.'' Math. Mag. 61, 1-23, 1988.Stoimenow, A. ``Kauffman Polynomials.'' http://www.informatik.hu-berlin.de/~stoimeno/ptab/k10.html.  Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m. Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.
|
![]() Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.
Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.