“Pascal's Triangle”的概念、定义、习题解题方法及翻译-数学辞典

单词

Pascal's Triangle

释义

Pascal's Triangle

A Triangle of numbers arranged in staggered rows such that

(1)

where

is a B. Pascal,

although it had been described centuries earlier by Chinese mathematician Yanghui (about 500 years earlier, in fact) andthe Arabian poet-mathematician Omar Khayyám. It is therefore known as the Yanghui Triangle in China. Startingwith

, the Triangle is

(Sloane's A007318). Pascal's Formula shows that each subsequent row is obtained by adding the two entries diagonally above,

(2)

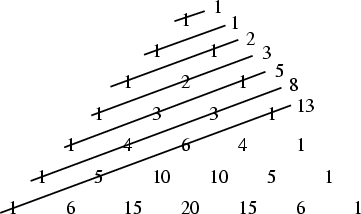
In addition, the ``Shallow Diagonals'' of Pascal's triangle sum to FibonacciNumbers,

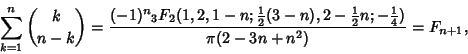(3)

where is a Generalized Hypergeometric Function.

Pascal's triangle contains the Figurate Numbers along its diagonals. It can be shown that

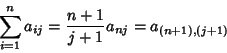(4)

and

(5)

The ``shallow diagonals'' sum to the Fibonacci Sequence, i.e.,






			(6)

In addition,

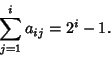(7)

It is also true that the first number after the 1 in each row divides all other numbers in that row Iff it is aPrime. If is the number of Odd terms in the first rows of the Pascal triangle, then

(8)

(Harborth 1976, Le Lionnais 1983).

The Binomial Coefficient mod 2 can be computed using the XOR operation XOR , makingPascal's triangle mod 2 very easy to construct. Pascal's triangle is unexpectedly connected with the construction ofregular Polygons and with the Sierpinski Sieve.

See also Bell Triangle, Binomial Coefficient, Binomial Theorem, Brianchon's Theorem,Catalan's Triangle, Clark's Triangle, Euler's Triangle, Fibonacci Number, Figurate NumberTriangle, Leibniz Harmonic Triangle, Number Triangle, Pascal's Formula, Polygon,Seidel-Entringer-Arnold Triangle, Sierpinski Sieve, Trinomial Triangle

References

Conway, J. H. and Guy, R. K. ``Pascal's Triangle.'' In The Book of Numbers. New York: Springer-Verlag, pp. 68-70, 1996.

Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 17, 1996.

Harborth, H. ``Number of Odd Binomial Coefficients.'' Not. Amer. Math. Soc. 23, 4, 1976.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 31, 1983.

Pappas, T. ``Pascal's Triangle, the Fibonacci Sequence & Binomial Formula,'' ``Chinese Triangle,'' and ``Probability and Pascal's Triangle.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 40-41 88, and 184-186, 1989.

Sloane, N. J. A. SequenceA007318/M0082in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Smith, D. E. A Source Book in Mathematics. New York: Dover, p. 86, 1984.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。