| 释义 |
Golden RatioA number often encountered when taking the ratios of distances in simple geometric figures such as the Decagon andDodecagon. It is denoted  , or sometimes , or sometimes 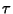 (which is an abbreviation of the Greek ``tome,'' meaning ``tocut''). (which is an abbreviation of the Greek ``tome,'' meaning ``tocut'').  is also known as the Divine Proportion, Golden Mean, and Golden Section and is aPisot-Vijayaraghavan Constant. It has surprising connections with ContinuedFractions and the Euclidean Algorithm for computing the Greatest Common Divisor of twoIntegers. is also known as the Divine Proportion, Golden Mean, and Golden Section and is aPisot-Vijayaraghavan Constant. It has surprising connections with ContinuedFractions and the Euclidean Algorithm for computing the Greatest Common Divisor of twoIntegers.
Given a Rectangle having sides in the ratio 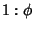 , ,  is defined such that partitioning the originalRectangle into a Square and new Rectangle results in a new Rectangle having sides with aratio is defined such that partitioning the originalRectangle into a Square and new Rectangle results in a new Rectangle having sides with aratio 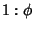 . Such a Rectangle is called a Golden Rectangle, and successive points dividing aGolden Rectangle into Squares lie on a Logarithmic Spiral. This figure is known as aWhirling Square. . Such a Rectangle is called a Golden Rectangle, and successive points dividing aGolden Rectangle into Squares lie on a Logarithmic Spiral. This figure is known as aWhirling Square. This means that
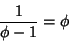 | (1) |
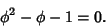 | (2) |
(Sloane's A001622).A geometric definition can be given in terms of the above figure. Let the ratio 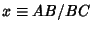 . The Numerator andDenominator can then be taken as . The Numerator andDenominator can then be taken as 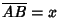 and and  without loss of generality. Now define theposition of without loss of generality. Now define theposition of  by by
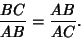 | (5) |
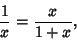 | (6) |
 | (7) |
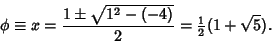 | (8) |
 is the ``most'' Irrational number because it has a Continued Fraction representation is the ``most'' Irrational number because it has a Continued Fraction representation
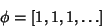 | (9) |
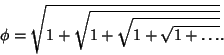 | (10) |
 gave the curious Continued Fraction identities gave the curious Continued Fraction identities
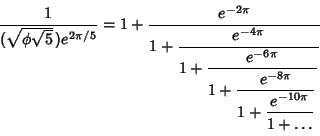 | (11) |
 | (12) |
The legs of a Golden Triangle are in a golden ratio to its base. In fact, this was the method used by Pythagorasto construct  . Euclid used the following construction. . Euclid used the following construction. Draw the Square 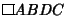 , call , call 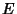 the Midpoint of the Midpoint of 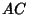 , so that , so that  . Now draw the segment . Now draw the segment , which has length , which has length
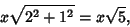 | (13) |
 with this length. Now construct with this length. Now construct  , then , then
 | (14) |
The ratio of the Circumradius to the length of the side of a Decagon is also  , ,
 | (15) |
In the figure above, three Triangles can be Inscribed in the Rectangle 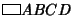 ofarbitrary aspect ratio ofarbitrary aspect ratio 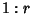 such that the three Right Triangles have equal areas by dividing such that the three Right Triangles have equal areas by dividing 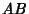 and and 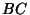 in the golden ratio. Then in the golden ratio. Then
which are all equal.
The golden ratio also satisfies the Recurrence Relation
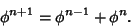 | (19) |
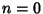 gives gives
 | (20) |
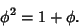 | (21) |
 (when the root with the plus sign is used). Squaring gives (when the root with the plus sign is used). Squaring gives
and so on.
For the difference equations
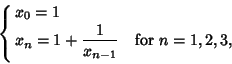 | (24) |
 is also given by is also given by
 | (25) |
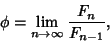 | (26) |
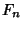 is the is the  th Fibonacci Number. th Fibonacci Number.
The Substitution Map
gives
 | (29) |
 | (30) |
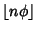 and and 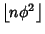 . The sequence also has many connections with theFibonacci Numbers. . The sequence also has many connections with theFibonacci Numbers.
Salem showed that the set of Pisot-Vijayaraghavan Constants is closed, with  the smallest accumulation pointof the set (Le Lionnais 1983). the smallest accumulation pointof the set (Le Lionnais 1983). See also Beraha Constants, Decagon, Five Disks Problem, Golden Ratio Conjugate, GoldenTriangle, Icosidodecahedron, Noble Number, Pentagon, Pentagram, Phi Number System,Secant Method
References
 Golden Ratio Golden RatioBoyer, C. B. History of Mathematics. New York: Wiley, p. 56, 1968. Coxeter, H. S. M. ``The Golden Section, Phyllotaxis, and Wythoff's Game.'' Scripta Mathematica 19, 135-143, 1953. Dixon, R. Mathographics. New York: Dover, pp. 30-31 and 50, 1991. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/cntfrc/cntfrc.html Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/gold/gold.html Gardner, M. ``Phi: The Golden Ratio.'' Ch. 8 in The Second Scientific American Book of Mathematical Puzzles & Diversions, A New Selection. New York: Simon and Schuster, 1961. Gardner, M. ``Notes on a Fringe-Watcher: The Cult of the Golden Ratio.'' Skeptical Inquirer 18, 243-247, 1994. Herz-Fischler, R. A Mathematical History of the Golden Number. New York: Dover, 1998. Huntley, H. E. The Divine Proportion. New York: Dover, 1970. Knott, R. ``Fibonacci Numbers and the Golden Section.'' http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 40, 1983. Markowsky, G. ``Misconceptions About the Golden Ratio.'' College Math. J. 23, 2-19, 1992. Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 122-134, 1990. Pappas, T. ``Anatomy & the Golden Section.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 32-33, 1989. Ramanathan, K. G. ``On Ramanujan's Continued Fraction.'' Acta. Arith. 43, 209-226, 1984. Sloane, N. J. A. SequencesA003849,A000012/M0003,A000201/M2322,A001622/M4046,A001950/M1332in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
![]() , or sometimes
, or sometimes ![]() (which is an abbreviation of the Greek ``tome,'' meaning ``tocut'').
(which is an abbreviation of the Greek ``tome,'' meaning ``tocut''). ![]() is also known as the Divine Proportion, Golden Mean, and Golden Section and is aPisot-Vijayaraghavan Constant. It has surprising connections with ContinuedFractions and the Euclidean Algorithm for computing the Greatest Common Divisor of twoIntegers.
is also known as the Divine Proportion, Golden Mean, and Golden Section and is aPisot-Vijayaraghavan Constant. It has surprising connections with ContinuedFractions and the Euclidean Algorithm for computing the Greatest Common Divisor of twoIntegers.![]() ,
, ![]() is defined such that partitioning the originalRectangle into a Square and new Rectangle results in a new Rectangle having sides with aratio
is defined such that partitioning the originalRectangle into a Square and new Rectangle results in a new Rectangle having sides with aratio ![]() . Such a Rectangle is called a Golden Rectangle, and successive points dividing aGolden Rectangle into Squares lie on a Logarithmic Spiral. This figure is known as aWhirling Square.
. Such a Rectangle is called a Golden Rectangle, and successive points dividing aGolden Rectangle into Squares lie on a Logarithmic Spiral. This figure is known as aWhirling Square.
![]() . The Numerator andDenominator can then be taken as
. The Numerator andDenominator can then be taken as ![]() and
and ![]() without loss of generality. Now define theposition of
without loss of generality. Now define theposition of ![]() by
by![]() is the ``most'' Irrational number because it has a Continued Fraction representation
is the ``most'' Irrational number because it has a Continued Fraction representation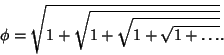
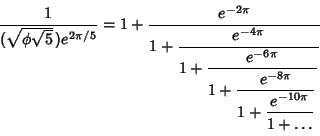

![]() . Euclid used the following construction.
. Euclid used the following construction.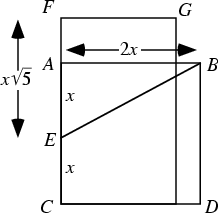
![]() , call
, call ![]() the Midpoint of
the Midpoint of ![]() , so that
, so that ![]() . Now draw the segment
. Now draw the segment![]() , which has length
, which has length![]() ,
,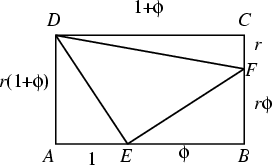
![]() ofarbitrary aspect ratio
ofarbitrary aspect ratio ![]() such that the three Right Triangles have equal areas by dividing
such that the three Right Triangles have equal areas by dividing ![]() and
and ![]() in the golden ratio. Then
in the golden ratio. Then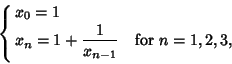
![]() the smallest accumulation pointof the set (Le Lionnais 1983).
the smallest accumulation pointof the set (Le Lionnais 1983).![]() Golden Ratio
Golden Ratio