| 释义 |
CurvatureIn general, there are two important types of curvature: Extrinsic Curvature and Intrinsic Curvature. TheExtrinsic Curvature of curves in 2- and 3-space was the first type of curvature to be studied historically,culminating in the Frenet Formulas, which describe a Space Curve entirely in terms of its ``curvature,''Torsion, and the initial starting point and direction.
After the curvature of 2- and 3-D curves was studied, attention turned to the curvature of surfaces in 3-space. The maincurvatures which emerged from this scrutiny are the Mean Curvature, Gaussian Curvature, and theWeingarten Map. Mean Curvature was the most important for applications at the time and was the most studied,but Gauß  was the first to recognize the importance of the Gaussian Curvature. was the first to recognize the importance of the Gaussian Curvature.
Because Gaussian Curvature is ``intrinsic,'' it is detectable to 2-dimensional ``inhabitants'' of the surface, whereasMean Curvature and the Weingarten Map are not detectable to someone who can't study the 3-dimensional spacesurrounding the surface on which he resides. The importance of Gaussian Curvature to an inhabitant is that it controlsthe surface Area of Spheres around the inhabitant.
Riemann  and many others generalized the concept of curvature to Sectional Curvature, Scalar Curvature,the Riemann Tensor, Ricci Curvature, and a host of other Intrinsic andExtrinsic Curvatures. General curvatures no longer need to be numbers, and can take the form ofa Map, Group, Groupoid, tensor field, etc. and many others generalized the concept of curvature to Sectional Curvature, Scalar Curvature,the Riemann Tensor, Ricci Curvature, and a host of other Intrinsic andExtrinsic Curvatures. General curvatures no longer need to be numbers, and can take the form ofa Map, Group, Groupoid, tensor field, etc.
The simplest form of curvature and that usually first encountered in Calculus is an Extrinsic Curvature. In 2-D,let a Plane Curve be given by Cartesian parametric equations 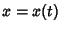 and and 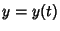 . Then the curvature . Then the curvature 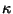 is defined by is defined by
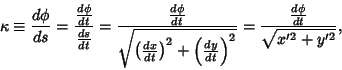 | (1) |
 is the Polar Angle and is the Polar Angle and  is the Arc Length. As can readily be seen from the definition, curvaturetherefore has units of inverse distance. The is the Arc Length. As can readily be seen from the definition, curvaturetherefore has units of inverse distance. The 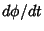 derivative in the above equation can be eliminated by using theidentity derivative in the above equation can be eliminated by using theidentity
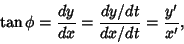 | (2) |
 | (3) |
Combining (2) and (4) gives
 | (5) |
For a 2-D curve written in the form 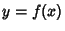 , the equation of curvature becomes , the equation of curvature becomes
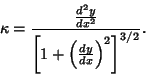 | (6) |
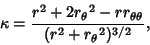 | (7) |
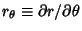 (Gray 1993). In Pedal Coordinates, the curvature is given by (Gray 1993). In Pedal Coordinates, the curvature is given by
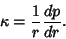 | (8) |
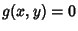 is given by is given by
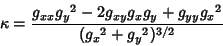 | (9) |
Now consider a parameterized Space Curve  in 3-D for which the Tangent Vector in 3-D for which the Tangent Vector 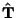 is defined as is defined as
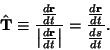 | (10) |
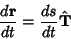 | (11) |
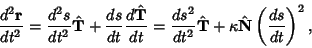 | (12) |
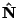 is the Normal Vector. But is the Normal Vector. But
 | (14) |
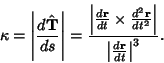 | (15) |
The curvature of a 2-D curve is related to the Radius of Curvature of the curve's Osculating Circle. Consider a Circle specified parametrically by
 | (16) |
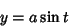 | (17) |
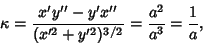 | (18) |
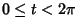 , the Arc Length is , the Arc Length is
so 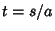 and the equations of the Circle can be rewritten as and the equations of the Circle can be rewritten as
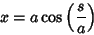 | (20) |
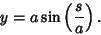 | (21) |
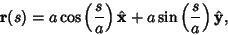 | (22) |
 | (23) |
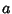 by by
as expected.
Four very important derivative relations in differential geometry related to the Frenet Formulas are
where T is the Tangent Vector, N is the Normal Vector, B is the Binormal Vector,and 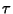 is the Torsion (Coxeter 1969, p. 322). is the Torsion (Coxeter 1969, p. 322).
The curvature at a point on a surface takes on a variety of values as the Plane through the normal varies. As 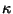 varies, it achieves a minimum and a maximum (which are in perpendicular directions) known as the Principal Curvatures. As shown in Coxeter (1969, pp. 352-353), varies, it achieves a minimum and a maximum (which are in perpendicular directions) known as the Principal Curvatures. As shown in Coxeter (1969, pp. 352-353),
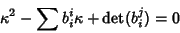 | (29) |
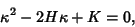 | (30) |
 is the Gaussian Curvature, is the Gaussian Curvature, 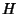 is the Mean Curvature, and det denotes the Determinant. is the Mean Curvature, and det denotes the Determinant.
The curvature 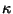 is sometimes called the First Curvature and the Torsion is sometimes called the First Curvature and the Torsion 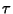 the Second Curvature. In addition, a Third Curvature (sometimes called TotalCurvature) the Second Curvature. In addition, a Third Curvature (sometimes called TotalCurvature)
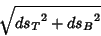 | (31) |
References
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.Fischer, G. (Ed.). Plates 79-85 in Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume. Braunschweig, Germany: Vieweg, pp. 74-81, 1986. Gray, A. ``Curvature of Curves in the Plane,'' ``Drawing Plane Curves with Assigned Curvature,'' and ``Drawing Space Curves with Assigned Curvature.'' §1.5, 6.4, and 7.8 in Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 11-13, 68-69, 113-118, and 145-147, 1993. Kreyszig, E. ``Principal Normal, Curvature, Osculating Circle.'' §12 in Differential Geometry. New York: Dover, pp. 34-36, 1991. Yates, R. C. ``Curvature.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 60-64, 1952. |
![]() was the first to recognize the importance of the Gaussian Curvature.
was the first to recognize the importance of the Gaussian Curvature. ![]() and many others generalized the concept of curvature to Sectional Curvature, Scalar Curvature,the Riemann Tensor, Ricci Curvature, and a host of other Intrinsic andExtrinsic Curvatures. General curvatures no longer need to be numbers, and can take the form ofa Map, Group, Groupoid, tensor field, etc.
and many others generalized the concept of curvature to Sectional Curvature, Scalar Curvature,the Riemann Tensor, Ricci Curvature, and a host of other Intrinsic andExtrinsic Curvatures. General curvatures no longer need to be numbers, and can take the form ofa Map, Group, Groupoid, tensor field, etc.![]() and
and ![]() . Then the curvature
. Then the curvature ![]() is defined by
is defined by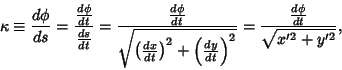
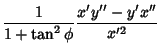
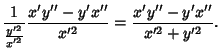
![]() , the equation of curvature becomes
, the equation of curvature becomes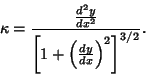
![]() in 3-D for which the Tangent Vector
in 3-D for which the Tangent Vector ![]() is defined as
is defined as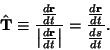
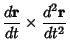
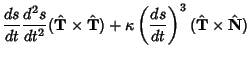
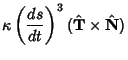
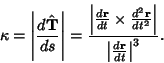
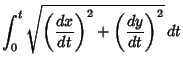
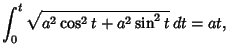
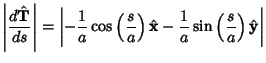
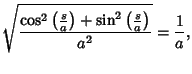
![]() varies, it achieves a minimum and a maximum (which are in perpendicular directions) known as the Principal Curvatures. As shown in Coxeter (1969, pp. 352-353),
varies, it achieves a minimum and a maximum (which are in perpendicular directions) known as the Principal Curvatures. As shown in Coxeter (1969, pp. 352-353),![]() is sometimes called the First Curvature and the Torsion
is sometimes called the First Curvature and the Torsion ![]() the Second Curvature. In addition, a Third Curvature (sometimes called TotalCurvature)
the Second Curvature. In addition, a Third Curvature (sometimes called TotalCurvature)