Gosper's Algorithm
An Algorithm for finding closed form Hypergeometric Identities. The algorithm treatssums whose successive terms have ratios which are Rational Functions. Not only does it decideconclusively whether there exists a hypergeometric sequence ![]() such that
such that
| (1) |
- 1. For the ratio
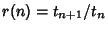 which is a Rational Function of
which is a Rational Function of  .
. - 2. Writewhere
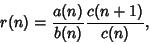
(2) 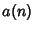 ,
, 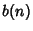 , and
, and 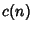 are polynomials satisfyingfor all nonnegative integers
are polynomials satisfyingfor all nonnegative integers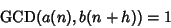
(3) 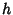 .
. - 3. Find a nonzero polynomial solution
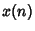 ofif one exists.
ofif one exists.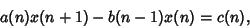
(4) - 4. Return
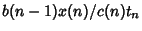 and stop.
and stop.
Petkovsek et al. (1996) describe the algorithm as ``one of the landmarks in the history of computerization of the problem ofclosed form summation.'' Gosper's algorithm is vital in the operation of Zeilberger's Algorithm and the machinery ofWilf-Zeilberger Pairs.
See also Hypergeometric Identity, Sister Celine's Method, Wilf-Zeilberger Pair, Zeilberger's Algorithm
References
Gessel, I. and Stanton, D. ``Strange Evaluations of Hypergeometric Series.'' SIAM J. Math. Anal. 13, 295-308, 1982. Gosper, R. W. ``Decision Procedure for Indefinite Hypergeometric Summation.'' Proc. Nat. Acad. Sci. USA 75, 40-42, 1978. Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994. Lafron, J. C. ``Summation in Finite Terms.'' In Computer Algebra Symbolic and Algebraic Computation, 2nd ed. (Ed. B. Buchberger, G. E. Collins, and R. Loos). New York: Springer-Verlag, 1983. Paule, P. and Schorn, M. ``A Mathematica Version of Zeilberger's Algorithm for Proving Binomial Coefficient Identities.'' J. Symb. Comput. 20, 673-698, 1995. Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. ``Gosper's Algorithm.'' Ch. 5 in A=B. Wellesley, MA: A. K. Peters, pp. 73-99, 1996. Zeilberger, D. ``The Method of Creative Telescoping.'' J. Symb. Comput. 11, 195-204, 1991.
- Bertrand's Paradox
- Bertrand's Postulate
- Bertrand's Problem
- Bertrand's Test
- Bertrand's Theorem
- Besov Space
- Bessel Differential Equation
- Bessel Function
- Bessel Function Fourier Expansion
- Bessel Function of the First Kind
- Bessel Function of the Second Kind
- Bessel Function of the Third Kind
- Bessel Polynomial
- Bessel's Correction
- Bessel's Finite Difference Formula
- Bessel's First Integral
- Bessel's Formula
- Bessel's Inequality
- Bessel's Interpolation Formula
- Bessel's Second Integral
- Bessel's Statistical Formula
- Beta
- Beta Distribution
- Beta Function
- Beta Function (Exponential)