| 释义 |
GradientThe gradient is a Vector operator denoted  and sometimes also called Del or Nabla.It is most often applied to a real function of three variables and sometimes also called Del or Nabla.It is most often applied to a real function of three variables  , and may be denoted , and may be denoted
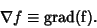 | (1) |
 | (2) |
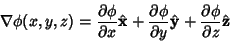 | (3) |
The direction of  is the orientation in which the Directional Derivative has the largest value and is the orientation in which the Directional Derivative has the largest value and is the value of that Directional Derivative. Furthermore, if is the value of that Directional Derivative. Furthermore, if 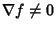 , then the gradientis Perpendicular to the Level Curve through , then the gradientis Perpendicular to the Level Curve through  if if  and Perpendicular to the levelsurface through and Perpendicular to the levelsurface through 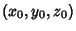 if if 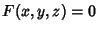 . .
In Tensor notation, let
 | (4) |
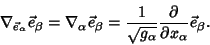 | (5) |
 , ,
 | (6) |
References
Arfken, G. ``Gradient,  '' and ``Successive Applications of '' and ``Successive Applications of  .'' §1.6 and 1.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 33-37 and 47-51, 1985. .'' §1.6 and 1.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 33-37 and 47-51, 1985. |
![]() and sometimes also called Del or Nabla.It is most often applied to a real function of three variables
and sometimes also called Del or Nabla.It is most often applied to a real function of three variables ![]() , and may be denoted
, and may be denoted![]() is the orientation in which the Directional Derivative has the largest value and
is the orientation in which the Directional Derivative has the largest value and![]() is the value of that Directional Derivative. Furthermore, if
is the value of that Directional Derivative. Furthermore, if ![]() , then the gradientis Perpendicular to the Level Curve through
, then the gradientis Perpendicular to the Level Curve through ![]() if
if ![]() and Perpendicular to the levelsurface through
and Perpendicular to the levelsurface through ![]() if
if ![]() .
. ![]() '' and ``Successive Applications of
'' and ``Successive Applications of ![]() .'' §1.6 and 1.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 33-37 and 47-51, 1985.
.'' §1.6 and 1.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 33-37 and 47-51, 1985.