| 释义 |
Graph (Graph Theory)A mathematical object composed of points known as Vertices or Nodes and linesconnecting some (possibly empty) Subset of them, known as Edges. The study of graphs is knownas Graph Theory. Graphs are 1-D Complexes, and there are always an Even number of OddNodes in a graph. The number of nonisomorphic graphs with  Nodes is givenby the Pólya Enumeration Theorem. The first few values for Nodes is givenby the Pólya Enumeration Theorem. The first few values for 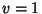 , 2, ..., are 1, 2,4, 11, 34, 156, 1044, ... (Sloane's A000088; see above figure). , 2, ..., are 1, 2,4, 11, 34, 156, 1044, ... (Sloane's A000088; see above figure).
Graph sums, differences, powers, and products can be defined, as can graph eigenvalues.
Before applying Pólya Enumeration Theorem, define the quantity
 | (1) |
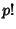 is the Factorial of is the Factorial of  , and the related polynomial , and the related polynomial
 | (2) |
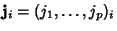 are all of the are all of the  -Vectors satisfying -Vectors satisfying
 | (3) |
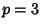 , the three possible values of , the three possible values of 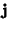 areTherefore, areTherefore,
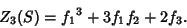 | (7) |
 , the first few values of , the first few values of  are given by are given by
 |  | 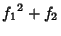 | (8) |  |  |  | (9) |  |  | 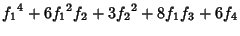 | (10) |  |  | 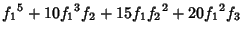 | | | |  | 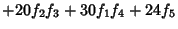 | (11) |  |  | 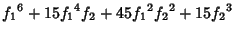 | | | |  | 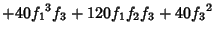 | | | |  |  | (12) |  |  | 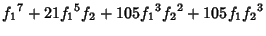 | | | |  | 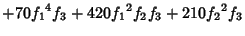 | | | |  | 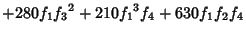 | | | |  |  | | | |  |  | (13) |
Application of the Pólya Enumeration Theorem then gives the formula where  is the Floor Function, is the Floor Function, 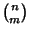 is a Binomial Coefficient, LCM is the Least CommonMultiple, GCD is the Greatest Common Divisor, and the Sum is a Binomial Coefficient, LCM is the Least CommonMultiple, GCD is the Greatest Common Divisor, and the Sum  is over all is over all 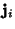 satisfying the sumidentity described above. The first few generating functions satisfying the sumidentity described above. The first few generating functions  are are
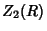 |  | 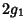 | (15) |  |  |  | (16) |  |  |  | (17) | 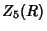 |  | 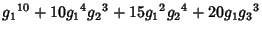 | | | |  |  | (18) | 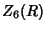 |  |  | | | |  | 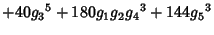 | | | |  | 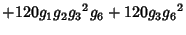 | | 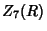 |  | 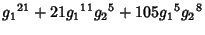 | (19) | | |  | 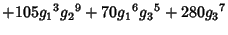 | | | |  | 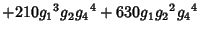 | | | |  |  | | | |  | 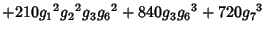 | | | |  | 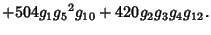 | (20) |
Letting 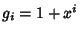 then gives a Polynomial then gives a Polynomial 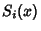 , which is a Generating Function for (i.e., the terms of , which is a Generating Function for (i.e., the terms of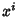 give) the number of graphs with give) the number of graphs with  Edges. The total number of graphs having Edges. The total number of graphs having  edges is edges is 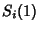 . The first few . The first few 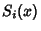 are are
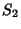 |  |  | (21) | 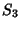 |  |  | (22) | 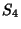 |  | 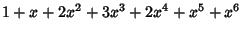 | (23) |  |  |  | | | |  | 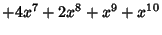 | (24) | 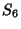 |  | 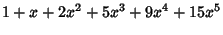 | | | |  | 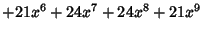 | | | |  |  | | | |  | 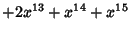 | (25) | 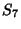 |  | 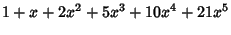 | | | |  | 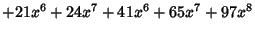 | | | |  | 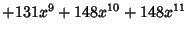 | | | |  | 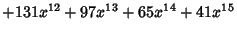 | | | |  |  | | | | | | (26) |
giving the number of graphs with  nodes as 1, 2, 4, 11, 34, 156, 1044, ... (Sloane's A000088). King and Palmer (cited in Read 1981)have calculated nodes as 1, 2, 4, 11, 34, 156, 1044, ... (Sloane's A000088). King and Palmer (cited in Read 1981)have calculated 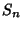 up to up to  , for which , for which | |  | (27) |
See also Bipartite Graph, Caterpillar Graph, Cayley Graph, Circulant Graph, Cocktail PartyGraph, Comparability Graph, Complement Graph, Complete Graph, Cone Graph, ConnectedGraph, Coxeter Graph, Cubical Graph, de Bruijn Graph, Digraph, Directed Graph,Dodecahedral Graph, Euler Graph, Extremal Graph, Gear Graph, Graceful Graph, GraphTheory, Hanoi Graph, Harary Graph, Harmonious Graph, Hoffman-Singleton Graph,Icosahedral Graph, Interval Graph, Isomorphic Graphs, Labeled Graph, Ladder Graph,Lattice Graph, Matchstick Graph, Minor Graph, Moore Graph, Null Graph, OctahedralGraph, Path Graph, Petersen Graphs, Planar Graph, Random Graph, Regular Graph,Sequential Graph, Simple Graph, Star Graph, Subgraph, Supergraph, SuperregularGraph, Sylvester Graph, Tetrahedral Graph, Thomassen Graph, Tournament,Triangular Graph, Turan Graph, Tutte's Graph, Universal Graph, Utility Graph, WebGraph, Wheel Graph
ReferencesBogomolny, A. ``Graph Puzzles.'' http://www.cut-the-knot.com/do_you_know/graphs2.html.Fujii, J. N. Puzzles and Graphs. Washington, DC: National Council of Teachers, 1966. Harary, F. ``The Number of Linear, Directed, Rooted, and Connected Graphs.'' Trans. Amer. Math. Soc. 78, 445-463, 1955. Pappas, T. ``Networks.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 126-127, 1989. Read, R. ``The Graph Theorists Who Count--and What They Count.'' In The Mathematical Gardner (Ed. D. Klarner). Boston, MA: Prindle, Weber, and Schmidt, pp. 326-345, 1981. Sloane, N. J. A. SequenceA000088/M1253in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and extended entry inSloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995. |
![]() Nodes is givenby the Pólya Enumeration Theorem. The first few values for
Nodes is givenby the Pólya Enumeration Theorem. The first few values for ![]() , 2, ..., are 1, 2,4, 11, 34, 156, 1044, ... (Sloane's A000088; see above figure).
, 2, ..., are 1, 2,4, 11, 34, 156, 1044, ... (Sloane's A000088; see above figure).
![]() then gives a Polynomial
then gives a Polynomial ![]() , which is a Generating Function for (i.e., the terms of
, which is a Generating Function for (i.e., the terms of![]() give) the number of graphs with
give) the number of graphs with ![]() Edges. The total number of graphs having
Edges. The total number of graphs having ![]() edges is
edges is ![]() . The first few
. The first few ![]() are
are