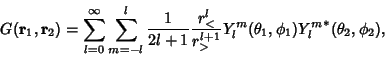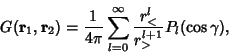| 释义 |
Green's Function--Poisson's EquationPoisson's Equation equation is
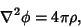 | (1) |
 is often called a potential function and is often called a potential function and  a density function, so the differential operator in this case is a density function, so the differential operator in this case is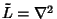 . As usual, we are looking for a Green's function . As usual, we are looking for a Green's function 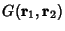 such that such that
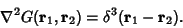 | (2) |
 | (3) |
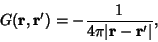 | (4) |
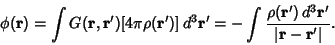 | (5) |
Expanding 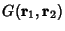 in the Spherical Harmonics in the Spherical Harmonics 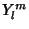 gives gives
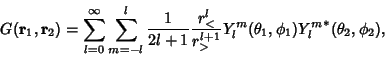 | (6) |
 and and  are Greater Than/Less Than Symbols. This expression simplifiesto are Greater Than/Less Than Symbols. This expression simplifiesto
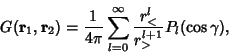 | (7) |
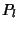 are Legendre Polynomials, and are Legendre Polynomials, and 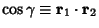 . Equations(6) and (7) give the addition theorem for Legendre Polynomials. . Equations(6) and (7) give the addition theorem for Legendre Polynomials.
In Cylindrical Coordinates, the Green's function is much more complicated,
 | (8) |
 and and  are Modified Bessel Functions of the Firstand Second Kinds (Arfken 1985). are Modified Bessel Functions of the Firstand Second Kinds (Arfken 1985).
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 485-486, 905, and 912, 1985. |
![]() in the Spherical Harmonics
in the Spherical Harmonics ![]() gives
gives