Groupoid
There are at least two definitions of ``groupoid'' currently in use.
The first type of groupoid is an algebraic structure on a Set with a Binary Operator. The only restriction onthe operator is Closure (i.e., applying the Binary Operator to two elements of a given set ![]() returns a valuewhich is itself a member of
returns a valuewhich is itself a member of ![]() ). Associativity, commutativity, etc., are not required (Rosenfeld 1968, pp. 88-103). Agroupoid can be empty. The numbers of nonisomorphic groupoids of this type having
). Associativity, commutativity, etc., are not required (Rosenfeld 1968, pp. 88-103). Agroupoid can be empty. The numbers of nonisomorphic groupoids of this type having ![]() elements are 1, 1, 10, 3330, 178981952,... (Sloane's A001329), and the numbers of nonisomorphic and nonantiisomorphic groupoids are 1, 7, 1734, 89521056, ...(Sloane's A001424). An associative groupoid is called a Semigroup.
elements are 1, 1, 10, 3330, 178981952,... (Sloane's A001329), and the numbers of nonisomorphic and nonantiisomorphic groupoids are 1, 7, 1734, 89521056, ...(Sloane's A001424). An associative groupoid is called a Semigroup.
The second type of groupoid is an algebraic structure first defined by Brandt (1926) and also known as a Virtual Group. A groupoid with base ![]() is a set
is a set ![]() with mappings
with mappings ![]() and
and ![]() from
from ![]() onto
onto ![]() and a partially defined binaryoperation
and a partially defined binaryoperation ![]() , satisfying the following four conditions:
, satisfying the following four conditions:
- 1.
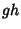 is defined only when
is defined only when 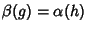 for certain maps
for certain maps 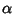 and
and 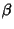 from
from  onto
onto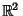 with
with 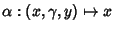 and
and 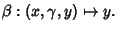
- 2. Associativity: If either
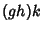 or
or 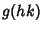 is defined, then so is the other and
is defined, then so is the other and .
. - 3. For each
 in
in  , there are left and right Identity Elements
, there are left and right Identity Elements 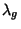 and
and 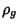 such that
such that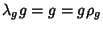 .
. - 4. Each
 in
in  has an inverse
has an inverse 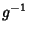 for which
for which 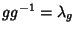 and
and 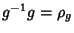
References
Brandt, W. ``Über eine Verallgemeinerung des Gruppengriffes.'' Math. Ann. 96, 360-366, 1926. Brown, R. ``From Groups to Groupoids: A Brief Survey.'' Bull. London Math. Soc. 19, 113-134, 1987. Brown, R. Topology: A Geometric Account of General Topology, Homotopy Types, and the Fundamental Groupoid. New York: Halsted Press, 1988. Higgins, P. J. Notes on Categories and Groupoids. London: Van Nostrand Reinhold, 1971. Ramsay, A.; Chiaramonte, R.; and Woo, L. ``Groupoid Home Page.'' http://amath-www.colorado.edu:80/math/researchgroups/groupoids/groupoids.shtml. Rosenfeld, A. An Introduction to Algebraic Structures. New York: Holden-Day, 1968. Sloane, N. J. A. SequencesA001424 andA001329/M4760in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995. Weinstein, A. ``Groupoids: Unifying Internal and External Symmetry.'' Not. Amer. Math. Soc. 43, 744-752, 1996.
- Prolate Spheroidal Coordinates
- Prolate Spheroidal Wave Function
- Pronic Number
- Proof
- Proofreading Mistakes
- Propeller
- Proper Cover
- Proper Divisor
- Proper Fraction
- Proper Integral
- Proper k-Coloring
- Proper Subset
- Proper Superset
- Proportional
- Proposition
- Propositional Calculus
- Prosthaphaeresis Formulas
- Proth's Theorem
- Protractor
- Prouhet's Problem
- Prussian Hat
- Prüfer Ring
- p-Series
- Pseudoanalytic Function
- Pseudocrosscap