| 释义 |
Göbel's SequenceConsider the Recurrence Relation
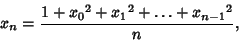 | (1) |
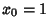 . The first few iterates of . The first few iterates of  are 1, 2, 3, 5, 10, 28, 154, ... (Sloane's A003504). The terms growextremely rapidly, but are given by the asymptotic formula are 1, 2, 3, 5, 10, 28, 154, ... (Sloane's A003504). The terms growextremely rapidly, but are given by the asymptotic formula
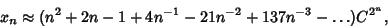 | (2) |
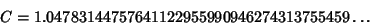 | (3) |
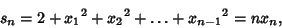 | (4) |
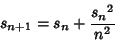 | (5) |
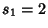 . Now, . Now, 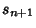 will be nonintegral Iff will be nonintegral Iff 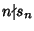 . The smallest . The smallest  for which for which (mod (mod  ) therefore gives the smallest nonintegral ) therefore gives the smallest nonintegral 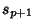 . In addition, since . In addition, since 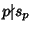 , ,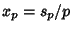 is also the smallest nonintegral is also the smallest nonintegral 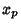 . .
For example, we have the sequences 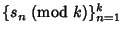 : :
 | (6) |
 | (7) |
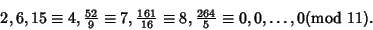 | (8) |
 shows that the first nonintegral shows that the first nonintegral  is is 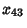 . Note that a direct verification of thisfact is impossible since . Note that a direct verification of thisfact is impossible since
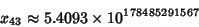 | (9) |
A sequence even more striking for remaining integral over many terms is the 3-Göbel sequence
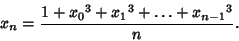 | (10) |
The Göbel sequences can be generalized to  powers by powers by
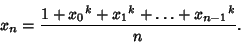 | (11) |
References
Guy, R. K. ``The Strong Law of Small Numbers.'' Amer. Math. Monthly 95, 697-712, 1988.Guy, R. K. ``A Recursion of Göbel.'' §E15 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 214-215, 1994. Sloane, N. J. A. SequencesA003504/M0728and A005166/M1551in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995. Zaiger, D. ``Solution: Day 5, Problem 3.'' http://www-groups.dcs.st-and.ac.uk/~john/Zagier/Solution5.3.html. |
![]() :
:![]() powers by
powers by