| 释义 |
Traveling Salesman ConstantsN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Let 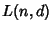 be the smallest Tour length for be the smallest Tour length for 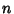 points in a points in a  -D Hypercube. Then there exists a smallestconstant -D Hypercube. Then there exists a smallestconstant 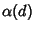 such that for all optimal Tours in the Hypercube, such that for all optimal Tours in the Hypercube,
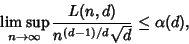 | (1) |
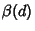 such that for almost all optimal tours in the Hypercube, such that for almost all optimal tours in the Hypercube,
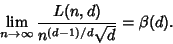 | (2) |
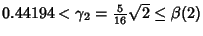 | | 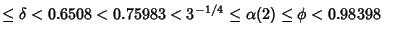 | (3) |
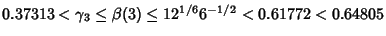 | | 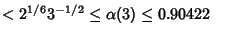 | (4) |
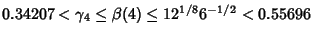 | | 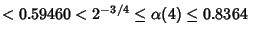 | (5) |
(Fejes Tóth 1940, Verblunsky 1951, Few 1955, Beardwood et al. 1959), where
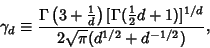 | (6) |
 is the Gamma Function, is the Gamma Function, 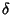 is an expression involving Struve Functionsand Neumann Functions, is an expression involving Struve Functionsand Neumann Functions,
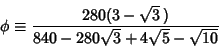 | (7) |
 | (8) |
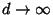 , ,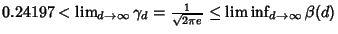 | | 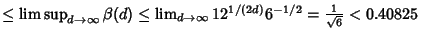 | (9) |
and
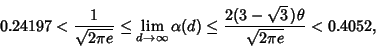 | (10) |
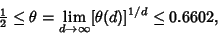 | (11) |
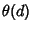 is the best Sphere Packing density in is the best Sphere Packing density in  -D space (Goddyn 1990, Moran 1984, Kabatyanskii andLevenshtein 1978). Steele and Snyder (1989) proved that the limit -D space (Goddyn 1990, Moran 1984, Kabatyanskii andLevenshtein 1978). Steele and Snyder (1989) proved that the limit 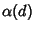 exists. exists.
Now consider the constant
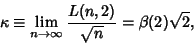 | (12) |
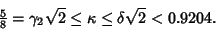 | (13) |
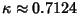 . .
A certain self-avoiding Space-Filling Curve is an optimal Tour through a set of 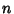 points, where points, where 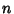 can bearbitrarily large. It has length can bearbitrarily large. It has length
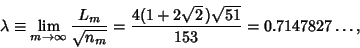 | (14) |
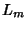 is the length of the curve at the is the length of the curve at the 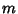 th iteration and th iteration and 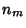 is the point-set size (Moscato and Norman). is the point-set size (Moscato and Norman).
References
Beardwood, J.; Halton, J. H.; and Hammersley, J. M. ``The Shortest Path Through Many Points.'' Proc. Cambridge Phil. Soc. 55, 299-327, 1959.Chartrand, G. ``The Salesman's Problem: An Introduction to Hamiltonian Graphs.'' §3.2 in Introductory Graph Theory. New York: Dover, pp. 67-76, 1985. Fejes Tóth, L. ``Über einen geometrischen Satz.'' Math. Zeit. 46, 83-85, 1940. Few, L. ``The Shortest Path and the Shortest Road Through 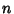 Points.'' Mathematika 2, 141-144, 1955. Points.'' Mathematika 2, 141-144, 1955. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/sales/sales.html Flood, M. ``The Travelling Salesman Problem.'' Operations Res. 4, 61-75, 1956. Goddyn, L. A. ``Quantizers and the Worst Case Euclidean Traveling Salesman Problem.'' J. Combin. Th. Ser. B 50, 65-81, 1990. Kabatyanskii, G. A. and Levenshtein, V. I. ``Bounds for Packing on a Sphere and in Space.'' Problems Inform. Transm. 14, 1-17, 1978. Karloff, H. J. ``How Long Can a Euclidean Traveling Salesman Tour Be?'' SIAM J. Disc. Math. 2, 91-99, 1989. Moran, S. ``On the Length of Optimal TSP Circuits in Sets of Bounded Diameter.'' J. Combin. Th. Ser. B 37, 113-141, 1984. Moscato, P. ``Fractal Instances of the Traveling Salesman Constant.'' http://www.ing.unlp.edu.ar/cetad/mos/FRACTAL_TSP_home.html Steele, J. M. and Snyder, T. L. ``Worst-Case Growth Rates of Some Classical Problems of Combinatorial Optimization.'' SIAM J. Comput. 18, 278-287, 1989. Verblunsky, S. ``On the Shortest Path Through a Number of Points.'' Proc. Amer. Math. Soc. 2, 904-913, 1951.
|
![]() be the smallest Tour length for
be the smallest Tour length for ![]() points in a
points in a ![]() -D Hypercube. Then there exists a smallestconstant
-D Hypercube. Then there exists a smallestconstant ![]() such that for all optimal Tours in the Hypercube,
such that for all optimal Tours in the Hypercube,![]() points, where
points, where ![]() can bearbitrarily large. It has length
can bearbitrarily large. It has length![]() Points.'' Mathematika 2, 141-144, 1955.
Points.'' Mathematika 2, 141-144, 1955.