“Hadamard Matrix”的概念、定义、习题解题方法及翻译-数学辞典

单词

Hadamard Matrix

释义

Hadamard Matrix

A class of Sylvester (1867) under the name of Anallagmatic Pavement. AHadamard matrix is a Square Matrix containing only 1s and s such that when any two columns or rows are placed sideby side, Half the adjacent cells are the same Sign and half the other (excepting from the count an -shaped``half-frame'' bordering the matrix on two sides which is composed entirely of 1s). When viewed as pavements, cells with 1sare colored black and those with s are colored white. Therefore, the Hadamard matrix must have white squares (s) and black squares (1s).

This is equivalent to the definition

(1)

where

is the

Identity Matrix. A Hadamard matrix of order

corresponds to a HadamardDesign (

Paley's Theorem guarantees that there always exists a Hadamard matrix when is divisible by 4 and of theform , where is an Odd Prime. In such cases, the Matrices can be constructed using aPaley Construction. The Paley Class is undefined for the following values of : 92, 116, 156, 172,184, 188, 232, 236, 260, 268, 292, 324, 356, 372, 376, 404, 412, 428, 436, 452, 472, 476, 508, 520, 532, 536, 584, 596, 604,612, 652, 668, 712, 716, 732, 756, 764, 772, 808, 836, 852, 856, 872, 876, 892, 904, 932, 940, 944, 952, 956, 964, 980, 988,996.

Sawade (1985) constructed . It is conjectured (and verified up to ) that exists forall Divisible by 4 (van Lint and Wilson 1993). However, the proof of this Conjecture remains an importantproblem in Coding Theory. The number of Hadamard matrices of order are 1, 1, 1, 5, 3, 60, 487, ...(Sloane's A007299).

If and are known, then can be obtained by replacing all 1s in by and all s by . For , Hadamard matrices with , 20, 28, 36, 44, 52, 60, 68, 76,84, 92, and 100 cannot be built up from lower order Hadamard matrices.

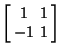			(2)

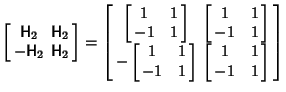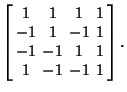			(3)

can be similarly generated from

. Hadamard matrices can also be expressed in terms of the Walsh Functions Cal and Sal

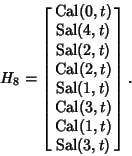(4)

Hadamard matrices can be used to make Error-Correcting Codes.

See also Hadamard Design, Paley Construction, Paley's Theorem, Walsh Function

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 107-109 and 274, 1987.

Beth, T.; Jungnickel, D.; and Lenz, H. Design Theory. New York: Cambridge University Press, 1986.

Colbourn, C. J. and Dinitz, J. H. (Eds.) ``Hadamard Matrices and Designs.'' Ch. 24 in CRC Handbook of Combinatorial Designs. Boca Raton, FL: CRC Press, pp. 370-377, 1996.

Geramita, A. V. Orthogonal Designs: Quadratic Forms and Hadamard Matrices. New York: Marcel Dekker, 1979.

Golomb, S. W. and Baumert, L. D. ``The Search for Hadamard Matrices.'' Amer. Math. Monthly 70, 12-17, 1963.

Hall, M. Jr. Combinatorial Theory, 2nd ed. New York: Wiley, p. 207, 1986.

Hedayat, A. and Wallis, W. D. ``Hadamard Matrices and Their Applications.'' Ann. Stat. 6, 1184-1238, 1978.

Kimura, H. ``Classification of Hadamard Matrices of Order 28.'' Disc. Math. 133, 171-180, 1994.

Kimura, H. ``Classification of Hadamard Matrices of Order 28 with Hall Sets.'' Disc. Math. 128, 257-269, 1994.

Kitis, L. ``Paley's Construction of Hadamard Matrices.''http://www.mathsource.com/cgi-bin/MathSource/Applications/Mathematics/0205-760.

Ogilvie, G. A. ``Solution to Problem 2511.'' Math. Questions and Solutions 10, 74-76, 1868.

Paley, R. E. A. C. ``On Orthogonal Matrices.'' J. Math. Phys. 12, 311-320, 1933.

Ryser, H. J. Combinatorial Mathematics. Buffalo, NY: Math. Assoc. Amer., pp. 104-122, 1963.

Sawade, K. ``A Hadamard Matrix of Order-268.'' Graphs Combinatorics 1, 185-187, 1985.

Seberry, J. and Yamada, M. ``Hadamard Matrices, Sequences, and Block Designs.'' Ch. 11 in Contemporary Design Theory: A Collection of Surveys (Eds. J. H. Dinitz and D. R. Stinson). New York: Wiley, pp. 431-560, 1992.

Sloane, N. J. A. SequenceA007299/M3736in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Spence, E. ``Classification of Hadamard Matrices of Order 24 and 28.'' Disc. Math 140, 185-243, 1995.

Sylvester, J. J. ``Thoughts on Orthogonal Matrices, Simultaneous Sign-Successions, and Tessellated Pavements in Two or More Colours, with Applications to Newton's Rule, Ornamental Tile-Work, and the Theory of Numbers.'' Phil. Mag. 34, 461-475, 1867.

Sylvester, J. J. ``Problem 2511.'' Math. Questions and Solutions 10, 74, 1868.

van Lint, J. H. and Wilson, R. M. A Course in Combinatorics. New York: Cambridge University Press, 1993.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。