| 释义 |
Pell EquationA special case of the quadratic Diophantine Equation having the form
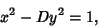 | (1) |
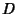 is a nonsquare Natural Number. Dörrie (1965) defines the equation as is a nonsquare Natural Number. Dörrie (1965) defines the equation as
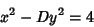 | (2) |
Pell equations, as well as the analogous equation with a minus sign on the right, can be solved by finding the ContinuedFraction 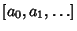 for for 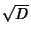 . (The trivial solution . (The trivial solution 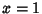 , , 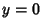 is ignored in all subsequent discussion.)Let is ignored in all subsequent discussion.)Let 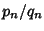 denote the denote the 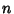 th Convergent th Convergent 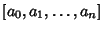 , then we are looking for a convergent which obeys theidentity , then we are looking for a convergent which obeys theidentity
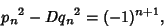 | (3) |
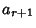 , where , where  , i.e., , i.e.,
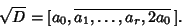 | (4) |
If 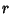 is Odd, then is Odd, then  is Positive and the solution in terms of smallest Integers is is Positive and the solution in terms of smallest Integers is  and and 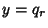 , where , where 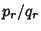 is the is the 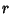 th Convergent. If th Convergent. If 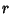 is Even, then is Even, then  is Negative, but is Negative, but
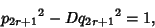 | (5) |
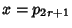 , , 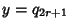 . Summarizing, . Summarizing,
 | (6) |
Given one solution 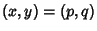 (which can be found as above), a whole family of solutions can be found by takingeach side to the (which can be found as above), a whole family of solutions can be found by takingeach side to the 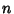 th Power, th Power,
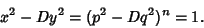 | (7) |
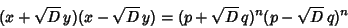 | (8) |
which gives the family of solutions
These solutions also hold for
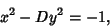 | (13) |
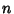 can take on only Odd values. can take on only Odd values.
The following table gives the smallest integer solutions 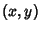 to the Pell equation with constant to the Pell equation with constant 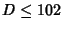 (Beiler 1966, p. 254). Square (Beiler 1966, p. 254). Square 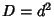 are not included, since they would result in an equation of the form are not included, since they would result in an equation of the form
 | (14) |
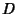 |  | 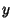 | 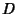 |  | 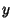 | | 2 | 3 | 2 | 54 | 485 | 66 | | 3 | 2 | 1 | 55 | 89 | 12 | | 5 | 9 | 4 | 56 | 15 | 2 | | 6 | 5 | 2 | 57 | 151 | 20 | | 7 | 8 | 3 | 58 | 19603 | 2574 | | 8 | 3 | 1 | 59 | 530 | 69 | | 10 | 19 | 6 | 60 | 31 | 4 | | 11 | 10 | 3 | 61 | 1766319049 | 226153980 | | 12 | 7 | 2 | 62 | 63 | 8 | | 13 | 649 | 180 | 63 | 8 | 1 | | 14 | 15 | 4 | 65 | 129 | 16 | | 15 | 4 | 1 | 66 | 65 | 8 | | 17 | 33 | 8 | 67 | 48842 | 5967 | | 18 | 17 | 4 | 68 | 33 | 4 | | 19 | 170 | 39 | 69 | 7775 | 936 | | 20 | 9 | 2 | 70 | 251 | 30 | | 21 | 55 | 12 | 71 | 3480 | 413 | | 22 | 197 | 42 | 72 | 17 | 2 | | 23 | 24 | 5 | 73 | 2281249 | 267000 | | 24 | 5 | 1 | 74 | 3699 | 430 | | 26 | 51 | 10 | 75 | 26 | 3 | | 27 | 26 | 5 | 76 | 57799 | 6630 | | 28 | 127 | 24 | 77 | 351 | 40 | | 29 | 9801 | 1820 | 78 | 53 | 6 | | 30 | 11 | 2 | 79 | 80 | 9 | | 31 | 1520 | 273 | 80 | 9 | 1 | | 32 | 17 | 3 | 82 | 163 | 18 | | 33 | 23 | 4 | 83 | 82 | 9 | | 34 | 35 | 6 | 84 | 55 | 6 | | 35 | 6 | 1 | 85 | 285769 | 30996 | | 37 | 73 | 12 | 86 | 10405 | 1122 | | 38 | 37 | 6 | 87 | 28 | 3 | | 39 | 25 | 4 | 88 | 197 | 21 | | 40 | 19 | 3 | 89 | 500001 | 53000 | | 41 | 2049 | 320 | 90 | 19 | 2 | | 42 | 13 | 2 | 91 | 1574 | 165 | | 43 | 3482 | 531 | 92 | 1151 | 120 | | 44 | 199 | 30 | 93 | 12151 | 1260 | | 45 | 161 | 24 | 94 | 2143295 | 221064 | | 46 | 24335 | 3588 | 95 | 39 | 4 | | 47 | 48 | 7 | 96 | 49 | 5 | | 48 | 7 | 1 | 97 | 62809633 | 6377352 | | 50 | 99 | 14 | 98 | 99 | 10 | | 51 | 50 | 7 | 99 | 10 | 1 | | 52 | 649 | 90 | 101 | 201 | 20 | | 53 | 66249 | 9100 | 102 | 101 | 10 |
The first few minimal values of  and and 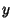 for nonsquare for nonsquare 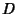 are 3, 2, 9, 5, 8, 3, 19, 10, 7, 649, ... (Sloane's A033313)and 2, 1, 4, 2, 3, 1, 6, 3, 2, 180, ... (Sloane's A033317), respectively. The values of are 3, 2, 9, 5, 8, 3, 19, 10, 7, 649, ... (Sloane's A033313)and 2, 1, 4, 2, 3, 1, 6, 3, 2, 180, ... (Sloane's A033317), respectively. The values of 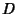 having having 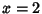 , 3, ... are3, 2, 15, 6, 35, 12, 7, 5, 11, 30, ... (Sloane's A033314) and the values of , 3, ... are3, 2, 15, 6, 35, 12, 7, 5, 11, 30, ... (Sloane's A033314) and the values of 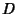 having having 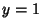 , 2, ... are 3, 2, 7, 5,23, 10, 47, 17, 79, 26, ... (Sloane's A033318). Values of the incrementally largest minimal , 2, ... are 3, 2, 7, 5,23, 10, 47, 17, 79, 26, ... (Sloane's A033318). Values of the incrementally largest minimal  are 3, 9, 19, 649, 9801,24335, 66249, ... (Sloane's A033315) which occur at are 3, 9, 19, 649, 9801,24335, 66249, ... (Sloane's A033315) which occur at  , 5, 10, 13, 29, 46, 53, 61, 109, 181, ... (Sloane's A033316). Values of the incrementally largest minimal , 5, 10, 13, 29, 46, 53, 61, 109, 181, ... (Sloane's A033316). Values of the incrementally largest minimal 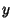 are 2, 4, 6, 180, 1820, 3588, 9100, 226153980, ... (Sloane's A033319),which occur at are 2, 4, 6, 180, 1820, 3588, 9100, 226153980, ... (Sloane's A033319),which occur at  , 5, 10, 13, 29, 46, 53, 61, ... (Sloane's A033320). , 5, 10, 13, 29, 46, 53, 61, ... (Sloane's A033320). See also Diophantine Equation, Diophantine Equation--Quadratic, Lagrange Number (Diophantine Equation)
References
Beiler, A. H. ``The Pellian.'' Ch. 22 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, pp. 248-268, 1966.Degan, C. F. Canon Pellianus. Copenhagen, Denmark, 1817. Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, 1965. Lagarias, J. C. ``On the Computational Complexity of Determining the Solvability or Unsolvability of the Equation 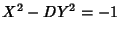 .'' Trans. Amer. Math. Soc. 260, 485-508, 1980. .'' Trans. Amer. Math. Soc. 260, 485-508, 1980. Sloane, N. J. A. Sequences A033313,A033314,A033315,A033316,A033317,A033318,A033319, andA033320in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Smarandache, F. ``Un metodo de resolucion de la ecuacion diofantica.'' Gaz. Math. 1, 151-157, 1988. Smarandache, F. `` Method to Solve the Diophantine Equation 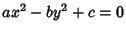 .'' In Collected Papers, Vol. 1. Lupton, AZ: Erhus University Press, 1996. .'' In Collected Papers, Vol. 1. Lupton, AZ: Erhus University Press, 1996. Stillwell, J. C. Mathematics and Its History. New York: Springer-Verlag, 1989. Whitford, E. E. Pell Equation. New York: Columbia University Press, 1912.
|
![]() for
for ![]() . (The trivial solution
. (The trivial solution ![]() ,
, ![]() is ignored in all subsequent discussion.)Let
is ignored in all subsequent discussion.)Let ![]() denote the
denote the ![]() th Convergent
th Convergent ![]() , then we are looking for a convergent which obeys theidentity
, then we are looking for a convergent which obeys theidentity![]() is Odd, then
is Odd, then ![]() is Positive and the solution in terms of smallest Integers is
is Positive and the solution in terms of smallest Integers is ![]() and
and ![]() , where
, where ![]() is the
is the ![]() th Convergent. If
th Convergent. If ![]() is Even, then
is Even, then ![]() is Negative, but
is Negative, but![]() (which can be found as above), a whole family of solutions can be found by takingeach side to the
(which can be found as above), a whole family of solutions can be found by takingeach side to the ![]() th Power,
th Power,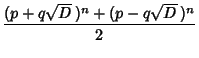
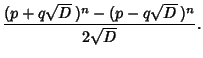
![]() to the Pell equation with constant
to the Pell equation with constant ![]() (Beiler 1966, p. 254). Square
(Beiler 1966, p. 254). Square ![]() are not included, since they would result in an equation of the form
are not included, since they would result in an equation of the form![]() and
and ![]() for nonsquare
for nonsquare ![]() are 3, 2, 9, 5, 8, 3, 19, 10, 7, 649, ... (Sloane's A033313)and 2, 1, 4, 2, 3, 1, 6, 3, 2, 180, ... (Sloane's A033317), respectively. The values of
are 3, 2, 9, 5, 8, 3, 19, 10, 7, 649, ... (Sloane's A033313)and 2, 1, 4, 2, 3, 1, 6, 3, 2, 180, ... (Sloane's A033317), respectively. The values of ![]() having
having ![]() , 3, ... are3, 2, 15, 6, 35, 12, 7, 5, 11, 30, ... (Sloane's A033314) and the values of
, 3, ... are3, 2, 15, 6, 35, 12, 7, 5, 11, 30, ... (Sloane's A033314) and the values of ![]() having
having ![]() , 2, ... are 3, 2, 7, 5,23, 10, 47, 17, 79, 26, ... (Sloane's A033318). Values of the incrementally largest minimal
, 2, ... are 3, 2, 7, 5,23, 10, 47, 17, 79, 26, ... (Sloane's A033318). Values of the incrementally largest minimal ![]() are 3, 9, 19, 649, 9801,24335, 66249, ... (Sloane's A033315) which occur at
are 3, 9, 19, 649, 9801,24335, 66249, ... (Sloane's A033315) which occur at ![]() , 5, 10, 13, 29, 46, 53, 61, 109, 181, ... (Sloane's A033316). Values of the incrementally largest minimal
, 5, 10, 13, 29, 46, 53, 61, 109, 181, ... (Sloane's A033316). Values of the incrementally largest minimal ![]() are 2, 4, 6, 180, 1820, 3588, 9100, 226153980, ... (Sloane's A033319),which occur at
are 2, 4, 6, 180, 1820, 3588, 9100, 226153980, ... (Sloane's A033319),which occur at ![]() , 5, 10, 13, 29, 46, 53, 61, ... (Sloane's A033320).
, 5, 10, 13, 29, 46, 53, 61, ... (Sloane's A033320).![]() .'' Trans. Amer. Math. Soc. 260, 485-508, 1980.
.'' Trans. Amer. Math. Soc. 260, 485-508, 1980.![]() .'' In Collected Papers, Vol. 1. Lupton, AZ: Erhus University Press, 1996.
.'' In Collected Papers, Vol. 1. Lupton, AZ: Erhus University Press, 1996.