| 释义 |
Halley's Irrational FormulaA Root-finding Algorithm which makes use of a third-order Taylor Series
 | (1) |
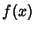 satisfies satisfies 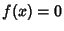 , so , so
 | (2) |
 | (3) |
 | (4) |
If the alternate form of the Quadratic Equation is used instead in solving (2), the iteration function becomesinstead
 | (5) |
 in Laguerre's Method. Numerically, the Sign in theDenominator is chosen to maximize its Absolute Value. Note that in the above equation, if in Laguerre's Method. Numerically, the Sign in theDenominator is chosen to maximize its Absolute Value. Note that in the above equation, if  , thenNewton's Method is recovered. This form of Halley's irrational formula has cubic convergence, and is usually foundto be substantially more stable than Newton's Method. However, it does run into difficulty when both , thenNewton's Method is recovered. This form of Halley's irrational formula has cubic convergence, and is usually foundto be substantially more stable than Newton's Method. However, it does run into difficulty when both 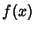 and and or or  and and  are simultaneously near zero.See also Halley's Method, Laguerre's Method, Newton's Method are simultaneously near zero.See also Halley's Method, Laguerre's Method, Newton's Method
References
Qiu, H. ``A Robust Examination of the Newton-Raphson Method with Strong Global Convergence Properties.'' Master's Thesis. University of Central Florida, 1993.Scavo, T. R. and Thoo, J. B. ``On the Geometry of Halley's Method.'' Amer. Math. Monthly 102, 417-426, 1995. |
