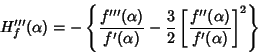| 释义 |
Halley's MethodAlso known as the Tangent Hyperbolas Method or Halley's Rational Formula. As in Halley's IrrationalFormula, take the second-order Taylor Polynomial
 | (1) |
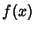 satisfies satisfies 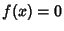 , so , so
 | (2) |
 | (3) |
 | (4) |
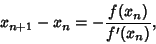 | (5) |
 | (6) |
 | (7) |
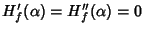 where where 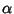 is a Root, so it is third order for simple zeros. Curiously, the third derivative is a Root, so it is third order for simple zeros. Curiously, the third derivative
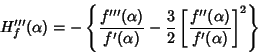 | (8) |
 . It may also be derived by using an Osculating Curve of the form . It may also be derived by using an Osculating Curve of the form
 | (9) |
which has solutions
so at a Root,  and and
 | (16) |
References
Scavo, T. R. and Thoo, J. B. ``On the Geometry of Halley's Method.'' Amer. Math. Monthly 102, 417-426, 1995. |