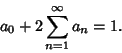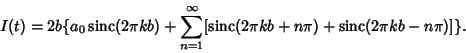“Hamming Function”的概念、定义、习题解题方法及翻译-数学辞典

单词

Hamming Function

释义

Hamming Function

An Apodization Function chosen to minimize the height of the highest sidelobe. The Hamming function is givenby

(1)

Its Full Width at Half Maximum is

. The corresponding Instrument Function is

(2)

This Apodization Function is close to the one produced by the requirement that the Apparatus Function goesto 0 at

. From Apodization Function, a general symmetric apodization function

can be written as aFourier Series

(3)

where the Coefficients satisfy

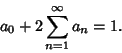(4)

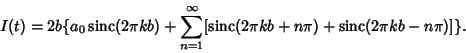The corresponding apparatus function is

(5)

To obtain an Apodization Function with zero at

, use

(6)

(7)

(8)

(9)


			(10)

			(11)

The FWHM is 1.81522, the peak is 1.08, the peak Negative and Positive sidelobes (in units of the peak) are

and 0.00734934, respectively.

See also Apodization Function, Hanning Function, Instrument Function

References

Blackman, R. B. and Tukey, J. W. ``Particular Pairs of Windows.'' In The Measurement of Power Spectra, From the Point of View of Communications Engineering. New York: Dover, pp. 98-99, 1959.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。