| 释义 |
Heat Conduction Equation--DiskTo solve the Heat Conduction Equation on a 2-D disk of radius 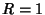 , try to separate the equation using , try to separate the equation using
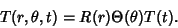 | (1) |
 and and  terms of the Laplacian in Spherical Coordinates gives terms of the Laplacian in Spherical Coordinates gives
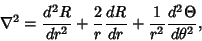 | (2) |
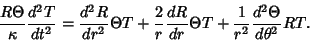 | (3) |
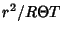 gives gives
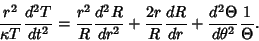 | (4) |
 term can be separated. term can be separated.
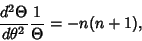 | (5) |
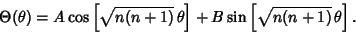 | (6) |
 | (7) |
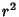 gives gives
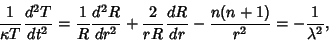 | (8) |
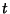 portion remains finite portion remains finite
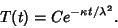 | (9) |
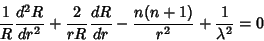 | (10) |
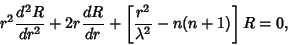 | (11) |
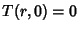 and the boundarycondition is and the boundarycondition is 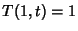 , the solution is , the solution is
 | (12) |
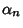 is the is the  th Positive zero of the Bessel Function of the First Kind th Positive zero of the Bessel Function of the First Kind  . . |
![]() , try to separate the equation using
, try to separate the equation using