“Helmholtz Differential Equation--Confocal Ellipsoidal Coordinates”的概念、定义、习题解题方法及翻译-数学辞典

单词

Helmholtz Differential Equation--Confocal Ellipsoidal Coordinates

释义

Helmholtz Differential Equation--Confocal Ellipsoidal Coordinates

Using the Notation of Byerly (1959, pp. 252-253), Laplace's Equation can be reduced to

(1)

where


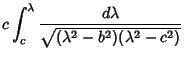			(2)

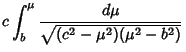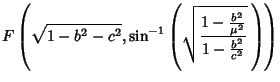			(3)

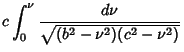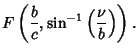			(4)

In terms of

, and

			(5)
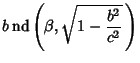			(6)
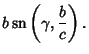			(7)

Equation (1) is not separable using a function of the form

(8)

but it is if we let

			(9)
			(10)
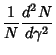			(11)

These give

			(12)
			(13)

and all others terms vanish. Therefore (1) can be broken up into the equations

			(14)
			(15)
			(16)

For future convenience, now write

			(17)
			(18)

then

			(19)
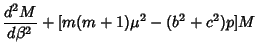			(20)
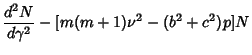			(21)

Now replace

, and

to obtain

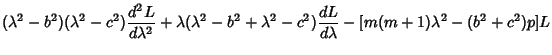			(22)
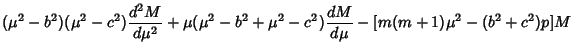			(23)
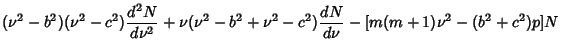			(24)

Each of these is a Lamé's Differential Equation, whose solution is called an Ellipsoidal Harmonic.Writing

			(25)
			(26)
			(27)

gives the solution to (1) as a product of Ellipsoidal Harmonics

(28)

References

Arfken, G. ``Confocal Ellipsoidal Coordinates .'' §2.15 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 117-118, 1970.

Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 251-258, 1959.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 663, 1953.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。