| 释义 |
Helmholtz Differential Equation--Elliptic Cylindrical CoordinatesIn Elliptic Cylindrical Coordinates, the Scale Factors are  , , 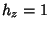 , and the separation functions are , and the separation functions are 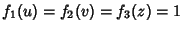 , giving aStäckel Determinant of , giving aStäckel Determinant of  . The Helmholtz differentialequation is . The Helmholtz differentialequation is
 | (1) |
 | (2) |
 | (3) |
 to give to give
 | (4) |
 part, part,
 | (5) |
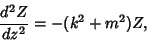 | (6) |
 | (7) |
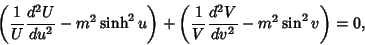 | (8) |
so
 | (11) |
 | (12) |
 | (13) |
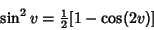 | (14) |
 | (15) |
 | (16) |
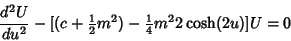 | (17) |
 | (18) |
 and and  , then these become , then these become
 | (19) |
 | (20) |
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 514 and 657, 1953. |
![]() ,
, ![]() , and the separation functions are
, and the separation functions are ![]() , giving aStäckel Determinant of
, giving aStäckel Determinant of ![]() . The Helmholtz differentialequation is
. The Helmholtz differentialequation is
