| 释义 |
Helmholtz Differential Equation--Spherical CoordinatesIn Spherical Coordinates, the Scale Factors are  , ,  , , 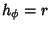 , andthe separation functions are , andthe separation functions are 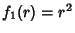 , , 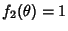 , ,  , giving a StäckelDeterminant of , giving a StäckelDeterminant of 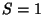 . The Laplacian is . The Laplacian is
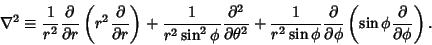 | (1) |
 | (2) |
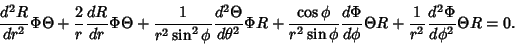 | (3) |
 , ,
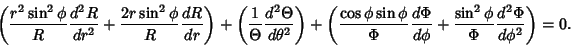 | (5) |
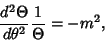 | (6) |
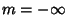 , ..., , ..., 
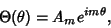 | (7) |
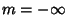 , ..., , ..., 
 | (8) |
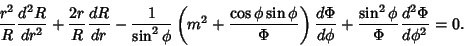 | (9) |
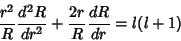 | (10) |
 | (11) |
But this is the Euler Differential Equation, so we try a series solution of the form
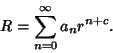 | (12) |
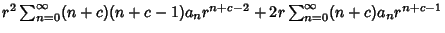 | | 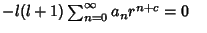 | (13) |
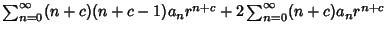 | | 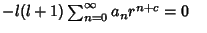 | (14) |
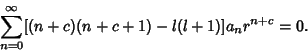 | (15) |
 . For the . For the 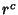 term (with term (with  ), ),
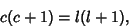 | (16) |
 and all other terms vanish. So and all other terms vanish. So  for for 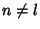 , , 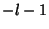 . Therefore, thesolution of the . Therefore, thesolution of the  component is given by component is given by
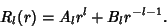 | (17) |
 | (18) |
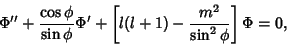 | (19) |
 and and  , ..., , ..., 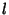 . The generalComplex solution is therefore . The generalComplex solution is therefore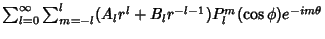 | | 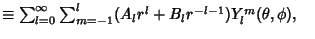 | (20) |
where
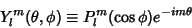 | (21) |
 | (22) |
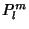 can be absorbed by can be absorbed by  and and 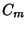 , so this equation may appear in theform , so this equation may appear in theform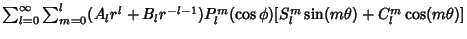 | |  | (23) |
where
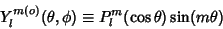 | (24) |
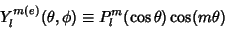 | (25) |
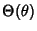 is constant and the solution of the is constant and the solution of the 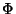 component is a Legendre Polynomial component is a Legendre Polynomial 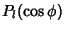 . Thegeneral solution is then . Thegeneral solution is then
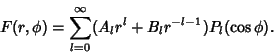 | (26) |
Actually, the equation is separable under the more general condition that 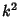 is of the form is of the form
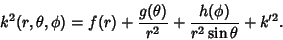 | (27) |
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 514 and 658, 1953. |
![]() ,
, ![]() ,
, ![]() , andthe separation functions are
, andthe separation functions are ![]() ,
, ![]() ,
, ![]() , giving a StäckelDeterminant of
, giving a StäckelDeterminant of ![]() . The Laplacian is
. The Laplacian is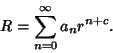
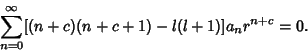

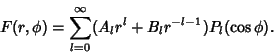
![]() is of the form
is of the form