| 释义 |
Covariant TensorA covariant tensor is a Tensor having specific transformation properties (c.f., a Contravariant Tensor). Toexamine the transformation properties of a covariant tensor, first consider the Gradient
 | (1) |
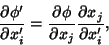 | (2) |
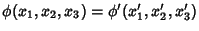 . Now let . Now let
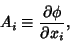 | (3) |
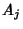 which transform according to which transform according to
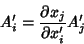 | (4) |
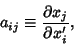 | (5) |
 | (6) |
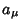 . .
Contravariant Tensors are a type of Tensor with differing transformation properties,denoted  . However, in 3-D Cartesian Coordinates, . However, in 3-D Cartesian Coordinates,
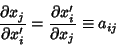 | (7) |
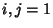 , 2, 3, meaning that contravariant and covariant tensors are equivalent. The two types of tensors do differin higher dimensions, however. Covariant Four-Vectors satisfy , 2, 3, meaning that contravariant and covariant tensors are equivalent. The two types of tensors do differin higher dimensions, however. Covariant Four-Vectors satisfy
 | (8) |
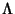 is a Lorentz Tensor. is a Lorentz Tensor.
To turn a Contravariant Tensor into a covariant tensor, use the Metric Tensor 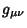 to write to write
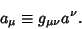 | (9) |
References
Arfken, G. ``Noncartesian Tensors, Covariant Differentiation.'' §3.8 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 158-164, 1985.Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 44-46, 1953. |
![]() . However, in 3-D Cartesian Coordinates,
. However, in 3-D Cartesian Coordinates,![]() to write
to write