| 释义 |
Hermite-Gauss QuadratureAlso called Hermite Quadrature. A Gaussian Quadrature over the interval 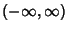 withWeighting Function withWeighting Function 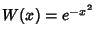 . The Abscissas for quadrature order . The Abscissas for quadrature order  are given by theroots of the Hermite Polynomials are given by theroots of the Hermite Polynomials 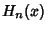 , which occur symmetrically about 0. TheWeights are , which occur symmetrically about 0. TheWeights are
 | (1) |
 is the Coefficient of is the Coefficient of  in in 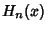 . For Hermite Polynomials, . For Hermite Polynomials,
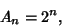 | (2) |
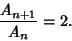 | (3) |
 | (4) |
Using the Recurrence Relation
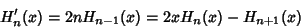 | (6) |
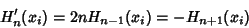 | (7) |
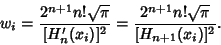 | (8) |
 | (9) |
 =12. =12. | 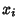 | 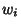 | | 2 | ± 0.707107 | 0.886227 | | 3 | 0 | 1.18164 | | | ± 1.22474 | 0.295409 | | 4 | ± 0.524648 | 0.804914 | | | ± 1.65068 | 0.0813128 | | 5 | 0 | 0.945309 | | | ± 0.958572 | 0.393619 | | | ± 2.02018 | 0.0199532 |
The Abscissas and weights can be computed analytically for small  . .
ReferencesBeyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 464, 1987.Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 327-330, 1956. |
![]() withWeighting Function
withWeighting Function ![]() . The Abscissas for quadrature order
. The Abscissas for quadrature order ![]() are given by theroots of the Hermite Polynomials
are given by theroots of the Hermite Polynomials ![]() , which occur symmetrically about 0. TheWeights are
, which occur symmetrically about 0. TheWeights are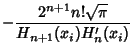
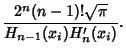
![]() .
.
