| 释义 |
Hermite PolynomialA set of Orthogonal Polynomials. The Hermite polynomials 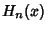 are illustrated above for are illustrated above for 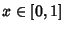 and and  , 2,..., 5. , 2,..., 5.
The Generating Function for Hermite polynomials is
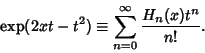 | (1) |
Since  , ,
Now define operators
It follows that
so
 | (8) |
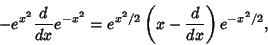 | (9) |
The Hermite Polynomials are related to the derivative of the Error Function by
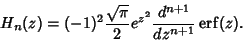 | (13) |
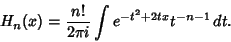 | (14) |
 with respect to the Weighting Function with respect to the Weighting Function 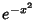
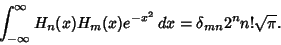 | (15) |
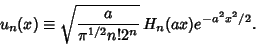 | (16) |
These obey the orthogonality conditions
if 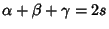 is Even and is Even and 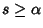 , , 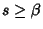 , and , and 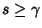 . Otherwise, thelast integral is 0 (Szegö 1975, p. 390). . Otherwise, thelast integral is 0 (Szegö 1975, p. 390).
They also satisfy the Recurrence Relations
 | (22) |
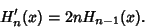 | (23) |
The Discriminant is
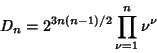 | (24) |
An interesting identity is
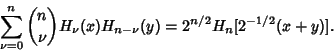 | (25) |
The first few Polynomials are
A class of generalized Hermite Polynomials 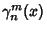 satisfying satisfying
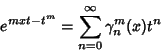 | (26) |
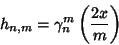 | (27) |
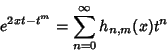 | (28) |
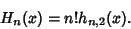 | (29) |
A modified version of the Hermite Polynomial is sometimes defined by
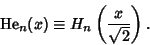 | (30) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.Arfken, G. ``Hermite Functions.'' §13.1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 712-721, 1985. Chebyshev, P. L. ``Sur le développement des fonctions à une seule variable.'' Bull. ph.-math., Acad. Imp. Sc. St. Pétersbourg 1, 193-200, 1859. Chebyshev, P. L. Oeuvres, Vol. 1. New York: Chelsea, pp. 49-508, 1987. Djordjevic, G. ``On Some Properties of Generalized Hermite Polynomials.'' Fib. Quart. 34, 2-6, 1996. Hermite, C. ``Sur un nouveau développement en série de fonctions.'' Compt. Rend. Acad. Sci. Paris 58, 93-100 and 266-273, 1864. Reprinted in Hermite, C. Oeuvres complètes, Vol. 2. Paris, pp. 293-308, 1908. Hermite, C. Oeuvres complètes, Vol. 3. Paris, p. 432, 1912. Iyanaga, S. and Kawada, Y. (Eds.). ``Hermite Polynomials.'' Appendix A, Table 20.IV in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1479-1480, 1980. Sansone, G. ``Expansions in Laguerre and Hermite Series.'' Ch. 4 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 295-385, 1991. Spanier, J. and Oldham, K. B. ``The Hermite Polynomials 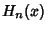 .'' Ch. 24 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 217-223, 1987. .'' Ch. 24 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 217-223, 1987. Subramanyan, P. R. ``Springs of the Hermite Polynomials.'' Fib. Quart. 28, 156-161, 1990. Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975. |
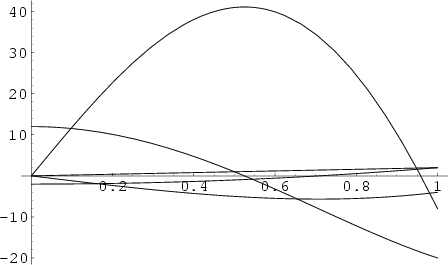
![]() are illustrated above for
are illustrated above for ![]() and
and ![]() , 2,..., 5.
, 2,..., 5.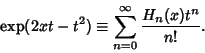
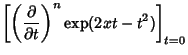
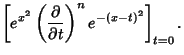
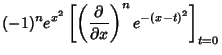
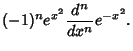
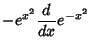

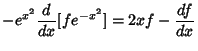
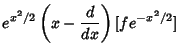
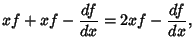
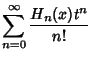
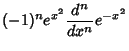

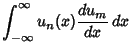
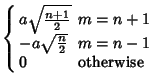
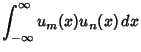
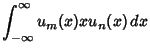
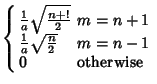

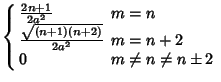
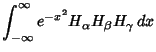
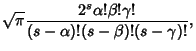
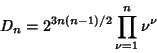
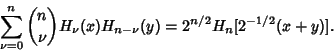

![]() satisfying
satisfying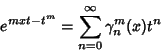
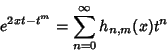
![]() .'' Ch. 24 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 217-223, 1987.
.'' Ch. 24 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 217-223, 1987.