| 释义 |
Hypergeometric FunctionA Generalized Hypergeometric Function  is a function which can be definedin the form of a Hypergeometric Series, i.e., a series for which the ratio of successive terms can be written is a function which can be definedin the form of a Hypergeometric Series, i.e., a series for which the ratio of successive terms can be written
 | (1) |
 in the Denominator is present for historical reasons of notation.) The function in the Denominator is present for historical reasons of notation.) The function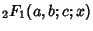 corresponding to corresponding to  , ,  is the first hypergeometric function to be studied (and, in general, arisesthe most frequently in physical problems), and so is frequently known as ``the'' hypergeometric equation. To confuse matterseven more, the term ``hypergeometric function'' is less commonly used to mean Closed Form. is the first hypergeometric function to be studied (and, in general, arisesthe most frequently in physical problems), and so is frequently known as ``the'' hypergeometric equation. To confuse matterseven more, the term ``hypergeometric function'' is less commonly used to mean Closed Form.
The hypergeometric functions are solutions to the Hypergeometric Differential Equation, which has a RegularSingular Point at the Origin. To derive the hypergeometric function based on the Hypergeometric DifferentialEquation, plug
into
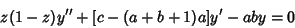 | (5) |
 | |  | (6) |
 | |  | (7) |
 | | 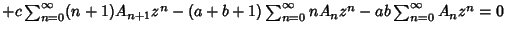 | (8) |
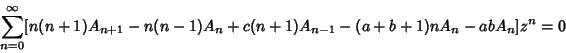 | (9) |
 | (10) |
 | (11) |
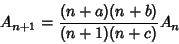 | (12) |
 | (13) |
where 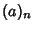 are Pochhammer Symbols. The hypergeometric series is convergent forReal are Pochhammer Symbols. The hypergeometric series is convergent forReal  , and for , and for  if if  . The complete solution to the HypergeometricDifferential Equation is . The complete solution to the HypergeometricDifferential Equation is
 | (15) |
Derivatives are given by
(Magnus and Oberhettinger 1949, p. 8). An integral giving the hypergeometric function is
 | (18) |
 in 1748. in 1748.
A hypergeometric function can be written using Euler's Hypergeometric Transformations
in any one of four equivalent forms
It can also be written as a linear combination | |  | (26) |
Kummer  found all six solutions (not necessarily regular at the origin) to the Hypergeometric DifferentialEquation, found all six solutions (not necessarily regular at the origin) to the Hypergeometric DifferentialEquation,
Applying Euler's Hypergeometric Transformations to the Kummer solutions then gives all 24 possible forms which are solutionsto the Hypergeometric Differential Equation
Goursat (1881) gives many hypergeometric transformation Formulas, including several cubic transformation Formulas.
Many functions of mathematical physics can be expressed as special cases of the hypergeometric functions. For example,
 | (27) |
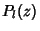 is a Legendre Polynomial. is a Legendre Polynomial.
 | (28) |
 | (29) |
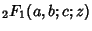 . Special values includeKummer's First Formula gives . Special values includeKummer's First Formula gives
 | (36) |
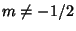 , , 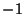 , ,  , .... Many additional identities are given by Abramowitz and Stegun (1972, p. 557). , .... Many additional identities are given by Abramowitz and Stegun (1972, p. 557).
Hypergeometric functions can be generalized to Generalized Hypergeometric Functions
 | (37) |
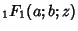 is called a Confluent Hypergeometric Function, and a function of the form is called a Confluent Hypergeometric Function, and a function of the form is called a Confluent Hypergeometric Limit Function.See also Appell Hypergeometric Function, is called a Confluent Hypergeometric Limit Function.See also Appell Hypergeometric Function,
Barnes' Lemma, Bradley's Theorem, Cayley's HypergeometricFunction Theorem, Clausen Formula, Closed Form, Confluent Hypergeometric Function, ConfluentHypergeometric Limit Function, Contiguous Function, Darling's Products, Generalized HypergeometricFunction, Gosper's Algorithm, Hypergeometric Identity, Hypergeometric Series, Jacobi Polynomial,Kummer's Formulas, Kummer's Quadratic Transformation, Kummer's Relation, Orr's Theorem,Ramanujan's Hypergeometric Identity, Saalschützian, Sister Celine's Method,Zeilberger's Algorithm
References
 Hypergeometric Functions Hypergeometric FunctionsAbramowitz, M. and Stegun, C. A. (Eds.). ``Hypergeometric Functions.'' Ch. 15 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 555-566, 1972. Arfken, G. ``Hypergeometric Functions.'' §13.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 748-752, 1985. Fine, N. J. Basic Hypergeometric Series and Applications. Providence, RI: Amer. Math. Soc., 1988. Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990. Gauss, C. F. ``Disquisitiones Generales Circa Seriem Infinitam 
 etc. Pars Prior.'' Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1813. etc. Pars Prior.'' Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1813. Gessel, I. and Stanton, D. ``Strange Evaluations of Hypergeometric Series.'' SIAM J. Math. Anal. 13, 295-308, 1982. Gosper, R. W. ``Decision Procedures for Indefinite Hypergeometric Summation.'' Proc. Nat. Acad. Sci. USA 75, 40-42, 1978. Goursat, M. E. ``Sur l'équation différentielle linéaire qui admet pour intégrale la série hypergéométrique.'' Ann. Sci. École Norm. Super. Sup. 10, S3-S142, 1881. Iyanaga, S. and Kawada, Y. (Eds.). ``Hypergeometric Functions and Spherical Functions.'' Appendix A, Table 18 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1460-1468, 1980. Kummer, E. E. ``Über die Hypergeometrische Reihe.'' J. für die Reine Angew. Mathematik 15, 39-83 and 127-172, 1837. Magnus, W. and Oberhettinger, F. Formulas and Theorems for the Special Functions of Mathematical Physics. New York: Chelsea, 1949. Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 541-547, 1953. Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, 1996. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Hypergeometric Functions.'' §6.12 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 263-265, 1992. Seaborn, J. B. Hypergeometric Functions and Their Applications. New York: Springer-Verlag, 1991. Snow, C. Hypergeometric and Legendre Functions with Applications to Integral Equations of Potential Theory. Washington, DC: U. S. Government Printing Office, 1952. Spanier, J. and Oldham, K. B. ``The Gauss Function  .'' Ch. 60 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 599-607, 1987. .'' Ch. 60 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 599-607, 1987.
|
![]() is a function which can be definedin the form of a Hypergeometric Series, i.e., a series for which the ratio of successive terms can be written
is a function which can be definedin the form of a Hypergeometric Series, i.e., a series for which the ratio of successive terms can be written


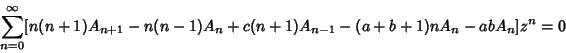





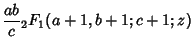





![]() Hypergeometric Functions
Hypergeometric Functions![]()
![]() etc. Pars Prior.'' Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1813.
etc. Pars Prior.'' Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1813.![]() .'' Ch. 60 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 599-607, 1987.
.'' Ch. 60 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 599-607, 1987.