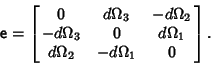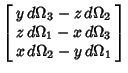| 释义 |
Infinitesimal RotationAn infinitesimal transformation of a Vector 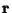 is given by is given by
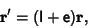 | (1) |
 is infinitesimal and I is the Identity Matrix. (Note that the infinitesimaltransformation may not correspond to an inversion, since inversion is a discontinuous process.) TheCommutativity of infinitesimal transformations is infinitesimal and I is the Identity Matrix. (Note that the infinitesimaltransformation may not correspond to an inversion, since inversion is a discontinuous process.) TheCommutativity of infinitesimal transformations 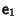 and and 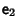 is established by theequivalence of is established by theequivalence of
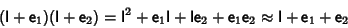 | (2) |
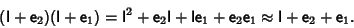 | (3) |
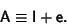 | (4) |
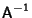 is then is then 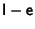 , since , since
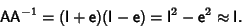 | (5) |
 | (6) |
 | (7) |
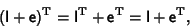 | (8) |
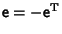 and the infinitesimal rotation is Antisymmetric. It must therefore have a Matrix of the form and the infinitesimal rotation is Antisymmetric. It must therefore have a Matrix of the form
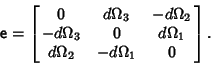 | (9) |
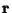 upon application of the Rotation Matrix is then upon application of the Rotation Matrix is then
 | (10) |
Therefore,
 | (13) |
 | (14) |
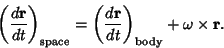 | (15) |
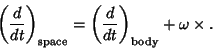 | (16) |
|
![]() is given by
is given by