Circumcenter
The center 
of a Triangle's Circumcircle. It can be found as the intersection of thePerpendicular Bisectors. If the Triangle is Acute,the circumcenter is in the interior of the Triangle. In a Right Triangle, the circumcenter is theMidpoint of the Hypotenuse.
 | (1) |
are the Midpoints of sides 
, 
is the Circumradius, and 
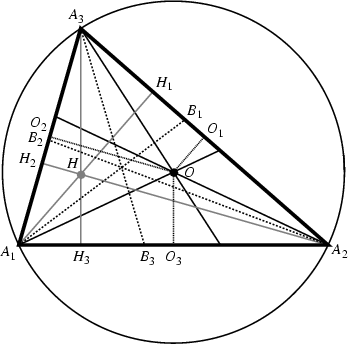
is theInradius (Johnson 1929, p. 190). The Trilinear Coordinates of the circumcenter are  | (2) |
 | (3) |
 | (4) |
. Given an interior point, the distances to theVertices are equal Iff this point is the circumcenter. It lies on the Brocard Axis.
The circumcenter and Orthocenter 
are Isogonal Conjugates.
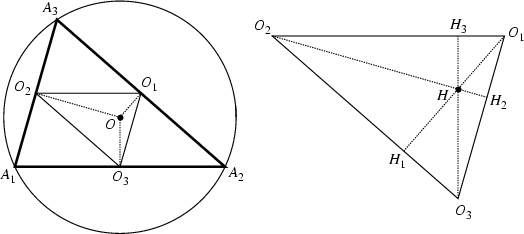
The Orthocenter of the Pedal Triangle 
formed by the Circumcenter concurs with the circumcenter itself, as illustrated above. The circumcenter also lies on the Euler Line.
References
Carr, G. S. Formulas and Theorems in Pure Mathematics, 2nd ed. New York: Chelsea, p. 623, 1970. Dixon, R. Mathographics. New York: Dover, p. 55, 1991. Eppstein, D. ``Circumcenters of Triangles.''http://www.ics.uci.edu/~eppstein/junkyard/circumcenter.html. Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, 1929. Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994. Kimberling, C. ``Circumcenter.''http://cedar.evansville.edu/~ck6/tcenters/class/ccenter.html.
- Dirichlet Divisor Problem
- Dirichlet Energy
- Dirichlet Eta Function
- Dirichlet Fourier Series Conditions
- Dirichlet Function
- Dirichlet Integrals
- Dirichlet Kernel
- Dirichlet Lambda Function
- Dirichlet L-Series
- Dirichlet Region
- Dirichlet's Boxing-In Principle
- Dirichlet's Box Principle
- Dirichlet Series
- Dirichlet's Formula
- Dirichlet's Lemma
- Dirichlet's Principle
- Dirichlet's Test
- Dirichlet's Theorem
- Dirichlet Structure Constant
- Dirichlet Tessellation
- Dirty Beam
- Dirty Map
- Disc
- Disconnected Form
- Disconnectivity