| 释义 |
Inverse TangentThe inverse tangent is also called the arctangent and is denoted either  or arctan or arctan 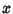 . It has theMaclaurin Series . It has theMaclaurin Series
 | (1) |
 is given by is given by
 | (2) |
 | (3) |
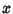 , and , and
 | (4) |
 . The inverse tangent is given in terms of other inverse trigonometric functions by . The inverse tangent is given in terms of other inverse trigonometric functions by
for Positive or Negative 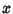 , and , and
for  . .
In terms of the Hypergeometric Function,
(Castellanos 1988). Castellanos (1986, 1988) also gives some curious formulas in terms of the Fibonacci Numbers,
where
and  is the largest Positive Root of is the largest Positive Root of
 | (19) |
The inverse tangent satisfies the addition Formula
 | (20) |
 | (21) |
 | (22) |
 | (23) |
 The inverse tangent Formulas areconnected with many interesting approximations to Pi The inverse tangent Formulas areconnected with many interesting approximations to Pi
 | (24) |
 gave gave
 | (25) |
 | (26) |
 | (27) |
 numerically, the following Arithmetic-Geometric Mean-like Algorithm canbe used. Let numerically, the following Arithmetic-Geometric Mean-like Algorithm canbe used. Let
Then compute
and the inverse tangent is given by
 | (32) |
An inverse tangent 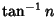 with integral with integral  is called reducible if it is expressible as a finite sum of the form is called reducible if it is expressible as a finite sum of the form
 | (33) |
 are Positive or Negative Integers and are Positive or Negative Integers and  are Integers are Integers  . .  is reducible Iff all the Prime factors of is reducible Iff all the Prime factors of  occur among the Prime factors of occur among the Prime factors of  for for  , ..., , ...,  . A second Necessary and Sufficient condition is that the largest Prime factorof . A second Necessary and Sufficient condition is that the largest Prime factorof  is less than is less than 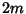 . Equivalent to the second condition is the statement that every Gregory Number . Equivalent to the second condition is the statement that every Gregory Number can be uniquely expressed as a sum in terms of can be uniquely expressed as a sum in terms of  s for which s for which  is a StérmerNumber (Conway and Guy 1996). To find this decomposition, write is a StérmerNumber (Conway and Guy 1996). To find this decomposition, write
 | (34) |
 | (35) |
 | (36) |
 | (37) |
 | (38) |
 | (39) |
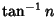 for for  . Conway and Guy (1996) give a similar table interms of Stérmer Numbers. . Conway and Guy (1996) give a similar table interms of Stérmer Numbers.
Arndt and Gosper give the remarkable inverse tangent identity
 | (40) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Inverse Circular Functions.'' §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79-83, 1972.Acton, F. S. ``The Arctangent.'' In Numerical Methods that Work, upd. and rev. Washington, DC: Math. Assoc. Amer., pp. 6-10, 1990. Arndt, J. ``Completely Useless Formulas.'' http://www.jjj.de/hfloat/hfloatpage.html#formulas. Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Item 137, Feb. 1972. Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987. Castellanos, D. ``Rapidly Converging Expansions with Fibonacci Coefficients.'' Fib. Quart. 24, 70-82, 1986. Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988. Conway, J. H. and Guy, R. K. ``Stérmer's Numbers.'' The Book of Numbers. New York: Springer-Verlag, pp. 245-248, 1996. Todd, J. ``A Problem on Arc Tangent Relations.'' Amer. Math. Monthly 56, 517-528, 1949.
|


![]() or arctan
or arctan ![]() . It has theMaclaurin Series
. It has theMaclaurin Series




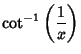








![]() with integral
with integral ![]() is called reducible if it is expressible as a finite sum of the form
is called reducible if it is expressible as a finite sum of the form