Isodynamic Points

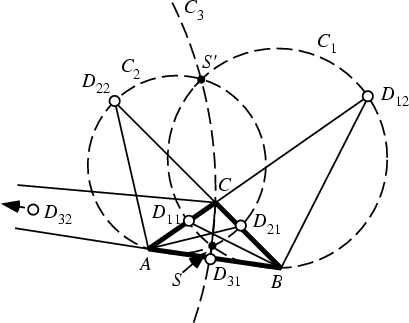
The first and second isodynamic points of a Triangle can be constructed by drawing the triangle's AngleBisectors and Exterior Angle Bisectors. Each pair of bisectors intersects aside of the triangle (or its extension) in two points and , for , 2, 3. The three Circles having, , and as Diameters are the Apollonius Circles ,, and . The points and in which the three Apollonius Circles intersect are the first and secondisodynamic points, respectively.

and have Triangle Center Functions

The isodynamic points are Isogonal Conjugates of the Isogonic Centers. They lie on theBrocard Axis. The distances from either isodynamic point to the Vertices are inverselyproportional to the sides. The Pedal Triangle of either isodynamic point is an Equilateral Triangle. AnInversion with either isodynamic point as the Inversion Center transforms the triangle into an Equilateral Triangle.

The Circle which passes through both the isodynamic points and the Centroid of a Triangle isknown as the Parry Circle.

References

Gallatly, W. The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, p. 106, 1913.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 295-297, 1929.

Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.

• Ludolph's Constant
• Ludwig's Inversion Formula
• Lukács Theorem
• Lune (Plane)
• Lune (Solid)
• Lune (Surface)
• Lunule
• Lusin's Theorem
• LUX Method
• Lyapunov Characteristic Exponent
• Lyapunov Characteristic Number
• Lyapunov Condition
• Lyapunov Dimension
• Lyapunov Function
• Lyapunov's First Theorem
• Lyapunov's Second Theorem
• Lyndon Word
• Lyons Group
• Léon Anne's Theorem
• Lévy Constant
• Lévy Distribution
• Lévy Flight
• Lévy Fractal
• Lévy Function
• Lévy Tapestry