| 释义 |
Krawtchouk PolynomialLet  be a Step Function with the Jump be a Step Function with the Jump
 | (1) |
 , 1, ..., , 1, ...,  , where , where 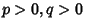 , and , and  . Then . Then
 | (2) |
 , 1, ..., , 1, ...,  . It has Weight Function . It has Weight Function
 | (3) |
 is the Gamma Function, Recurrence Relation is the Gamma Function, Recurrence Relation
 | (4) |
 | (5) |
 | (6) |
 is a Hermite Polynomial, and is related to the Hypergeometric Function by is a Hermite Polynomial, and is related to the Hypergeometric Function by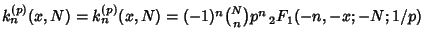 | |  | (7) |
See also Orthogonal Polynomials
References
Nikiforov, A. F.; Uvarov, V. B.; and Suslov, S. S. Classical Orthogonal Polynomials of a Discrete Variable. New York: Springer-Verlag, 1992.Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 35-37, 1975. Zelenkov, V. ``Krawtchouk Polynomial Home Page.'' http://www.isir.minsk.by/~zelenkov/physmath/kr_polyn/.
|
![]() be a Step Function with the Jump
be a Step Function with the Jump