Kronecker Symbol
An extension of the Jacobi Symbol 
to all Integers. It can be computed using thenormal rules for the Jacobi Symbol
 |  |  | |
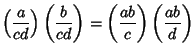|  | (1) |
plus additional rules for
, | (2) |
. The definition for 
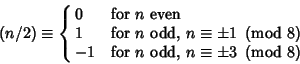is variously written as | (3) |
 | (4) |
for Singly Even Numbers 
and
, probably because no other values are needed in applications of the symbol involving theDiscriminants 
of Quadratic Fields, where 
and always satisfies 
.The Kronecker Symbol is a Real Character modulo 
, andis, in fact, essentially the only type of Real primitive character (Ayoub 1963).
References
Ayoub, R. G. An Introduction to the Analytic Theory of Numbers. Providence, RI: Amer. Math. Soc., 1963. Cohn, H. Advanced Number Theory. New York: Dover, p. 35, 1980.
- Rhombitruncated Icosidodecahedron
- Rhombohedron
- Rhomboid
- Rhomboidal Dodecahedron
- Rhombus
- Rhumb Line
- Ribbon Knot
- Ribet's Theorem
- Riccati-Bessel Functions
- Riccati Differential Equation
- Ricci Curvature
- Ricci Tensor
- Rice Distribution
- Richardson Extrapolation
- Richardson's Theorem
- Richard's Paradox
- Ridders' Method
- Ridge
- Riemann-Christoffel Tensor
- Riemann Curve Theorem
- Riemann Differential Equation
- Riemann Function
- Riemann Hypothesis
- Riemannian Geometry
- Riemannian Geometry (Non-Euclidean)