| 释义 |
Lagrange MultiplierUsed to find the Extremum of 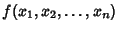 subject to the constraint subject to the constraint 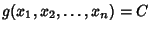 ,where ,where 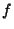 and and  are functions with continuous first Partial Derivatives on the OpenSet containing the curve are functions with continuous first Partial Derivatives on the OpenSet containing the curve 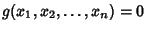 , and , and 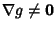 at any point on the curve(where at any point on the curve(where  is the Gradient). For an Extremum to exist, is the Gradient). For an Extremum to exist,
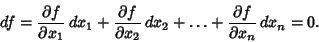 | (1) |
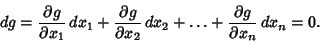 | (2) |
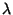 and add to (1), and add to (1),
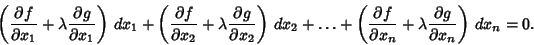 | (3) |
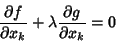 | (4) |
 , ..., , ..., 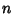 . The constant . The constant 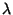 is called the Lagrange multiplier. For multiple constraints, is called the Lagrange multiplier. For multiple constraints,  , ,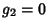 , ..., , ...,
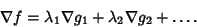 | (5) |
References
Arfken, G. ``Lagrange Multipliers.'' §17.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 945-950, 1985.
|
![]() subject to the constraint
subject to the constraint ![]() ,where
,where ![]() and
and ![]() are functions with continuous first Partial Derivatives on the OpenSet containing the curve
are functions with continuous first Partial Derivatives on the OpenSet containing the curve ![]() , and
, and ![]() at any point on the curve(where
at any point on the curve(where ![]() is the Gradient). For an Extremum to exist,
is the Gradient). For an Extremum to exist,