| 释义 |
Landau-Ramanujan ConstantN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Let  denote the number of Positive Integers not exceeding denote the number of Positive Integers not exceeding  which can be expressed as a sum oftwo squares, then which can be expressed as a sum oftwo squares, then
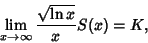 | (1) |
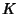 (also sometimes called (also sometimes called 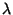 ) is ) is
 | (2) |
 . Flajolet and Vardi (1996) give a beautifulFormula with fast convergence . Flajolet and Vardi (1996) give a beautifulFormula with fast convergence
 | (3) |
 | (4) |
 is the Hurwitz Zeta Function. Landau proved the evenstronger fact is the Hurwitz Zeta Function. Landau proved the evenstronger fact
 | (5) |
Here,
 | (7) |
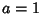 (the Lemniscate Constant to within a factor of 2 or 4),and (the Lemniscate Constant to within a factor of 2 or 4),and  is the Euler-Mascheroni Constant. is the Euler-Mascheroni Constant.
References
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 60-66, 1994.Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lr/lr.html Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript. 1996. http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps. Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 61-63, 1940. Landau, E. ``Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindeszahl der zu ihrer additiven Zusammensetzung erforderlichen Quadrate.'' Arch. Math. Phys. 13, 305-312, 1908. Shanks, D. ``The Second-Order Term in the Asymptotic Expansion of  .'' Math. Comput. 18, 75-86, 1964. .'' Math. Comput. 18, 75-86, 1964. Shanks, D. ``Non-Hypotenuse Numbers.'' Fibonacci Quart. 13, 319-321, 1975. Shanks, D. and Schmid, L. P. ``Variations on a Theorem of Landau. I.'' Math. Comput. 20, 551-569, 1966. Shiu, P. ``Counting Sums of Two Squares: The Meissel-Lehmer Method.'' Math. Comput. 47, 351-360, 1986.
|
![]() denote the number of Positive Integers not exceeding
denote the number of Positive Integers not exceeding ![]() which can be expressed as a sum oftwo squares, then
which can be expressed as a sum oftwo squares, then

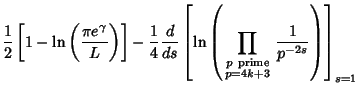
![]() .'' Math. Comput. 18, 75-86, 1964.
.'' Math. Comput. 18, 75-86, 1964.