Laplace Series
A function ![]() expressed as a double sum of Spherical Harmonics is called a Laplace series. Taking
expressed as a double sum of Spherical Harmonics is called a Laplace series. Taking ![]() as a Complex Function,
as a Complex Function,
 | (1) |
| (2) |
| (3) |
 | (4) |
For a Real series, consider
 | (5) |
| (6) |
| (7) |
 | (8) | ||
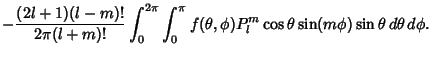 | (9) |
- Immersed Minimal Surface
- Immersion
- Impartial Game
- Implicit Function
- Implicit Function Theorem
- Implies
- Impossible Figure
- Impredicative
- Improper Integral
- Improper Node
- Improper Rotation
- Impulse Pair
- Impulse Symbol
- Inaccessible Cardinal
- Inaccessible Cardinals Axiom
- Inadmissible
- In-and-Out Curve
- Incenter
- Incenter-Excenter Circle
- Incidence Axioms
- Incidence Matrix
- Incident
- Incircle
- Inclusion-Exclusion Principle
- Inclusion Map