| 释义 |
Lebesgue Constants (Fourier Series)N.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Assume a function 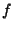 is integrable over the interval is integrable over the interval  and and 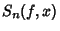 is the is the 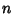 th partial sum of theFourier Series of th partial sum of theFourier Series of 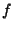 , so that , so that
and
 | (3) |
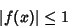 | (4) |
 , then , then
 | (5) |
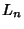 is the smallest possible constant for which this holds for all continuous is the smallest possible constant for which this holds for all continuous 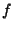 . The first few values of . The first few values of 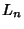 are are
Some Formulas for 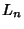 include include
(Zygmund 1959) and integral Formulas include
(Hardy 1942). For large 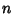 , ,
 | (12) |
This result can be generalized for an 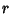 -differentiable function satisfying -differentiable function satisfying
 | (13) |
 . In this case, . In this case,
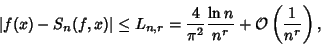 | (14) |
 | (15) |
Watson (1930) showed that
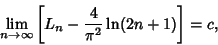 | (16) |
where 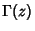 is the Gamma Function, is the Gamma Function,  is the Dirichlet Lambda Function, and is the Dirichlet Lambda Function, and  is the Euler-Mascheroni Constant. is the Euler-Mascheroni Constant.
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lbsg/lbsg.htmlHardy, G. H. ``Note on Lebesgue's Constants in the Theory of Fourier Series.'' J. London Math. Soc. 17, 4-13, 1942. Kolmogorov, A. N. ``Zur Grössenordnung des Restgliedes Fourierscher reihen differenzierbarer Funktionen.'' Ann. Math. 36, 521-526, 1935. Watson, G. N. ``The Constants of Landau and Lebesgue.'' Quart. J. Math. Oxford 1, 310-318, 1930. Zygmund, A. G. Trigonometric Series, 2nd ed., Vols. 1-2. Cambridge, England: Cambridge University Press, 1959.
|
![]() is integrable over the interval
is integrable over the interval ![]() and
and ![]() is the
is the ![]() th partial sum of theFourier Series of
th partial sum of theFourier Series of ![]() , so that
, so that
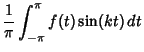






![]() -differentiable function satisfying
-differentiable function satisfying