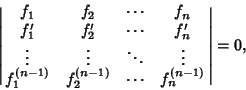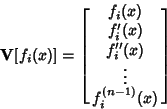| 释义 |
Linearly Dependent FunctionsThe  functions functions  , , 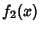 , ..., , ..., 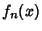 are linearly dependent if, for some are linearly dependent if, for some  , , 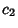 , ..., , ..., 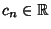 not all zero, not all zero,
 | (1) |
 in some interval in some interval  . If the functions are not linearly dependent,they are said to be linearly independent. Now, if the functions . If the functions are not linearly dependent,they are said to be linearly independent. Now, if the functions  , we can differentiate (1) upto , we can differentiate (1) upto 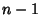 times. Therefore, linear dependence also requires times. Therefore, linear dependence also requires
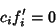 | (2) |
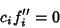 | (3) |
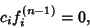 | (4) |
 , ..., , ...,  . These equations have a nontrivial solution Iff the Determinant . These equations have a nontrivial solution Iff the Determinant
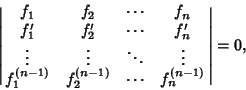 | (5) |
 . Ifthe Wronskian . Ifthe Wronskian 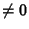 for any value for any value 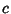 in the interval in the interval  , then the only solution possible for (2) is , then the only solution possible for (2) is  ( ( , ..., , ...,  ), and the functions are linearly independent. If, on the other hand, ), and the functions are linearly independent. If, on the other hand, 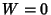 for a range, thefunctions are linearly dependent in the range. This is equivalent to stating that if the vectors for a range, thefunctions are linearly dependent in the range. This is equivalent to stating that if the vectors  ,..., ,..., 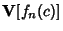 defined by defined by
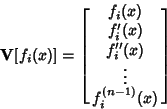 | (6) |
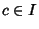 , then the functions , then the functions  are linearly independent in are linearly independent in  . .
References
Sansone, G. ``Linearly Independent Functions.'' §1.2 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 2-3, 1991. |
![]() functions
functions ![]() ,
, ![]() , ...,
, ..., ![]() are linearly dependent if, for some
are linearly dependent if, for some ![]() ,
, ![]() , ...,
, ..., ![]() not all zero,
not all zero,