| 释义 |
Lobatto QuadratureAlso called Radau Quadrature (Chandrasekhar 1960). A Gaussian Quadrature with Weighting Function 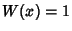 in which the endpoints of the interval in which the endpoints of the interval  are included in a total of are included in a total of 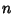 Abscissas, giving Abscissas, giving  freeabscissas. Abscissas are symmetrical about the origin, and the general Formula is freeabscissas. Abscissas are symmetrical about the origin, and the general Formula is
 | (1) |
 for for 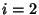 , ..., , ..., 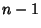 are the roots of the Polynomial are the roots of the Polynomial  , where , where is a Legendre Polynomial. The weights of the free abscissas are is a Legendre Polynomial. The weights of the free abscissas are
and of the endpoints are
 | (4) |
 | (5) |
 . Beyer (1987) gives a table of parameters up to . Beyer (1987) gives a table of parameters up to 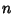 =11 and Chandrasekhar (1960) up to =11 and Chandrasekhar (1960) up to 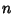 =9(although Chandrasekhar's =9(although Chandrasekhar's  for for 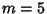 is incorrect). is incorrect).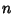 |  |  | | 3 | 0 | 1.33333 | | | ± 1 | 0.333333 | | 4 | ± 0.447214 | 0.833333 | | | ± 1 | 0.166667 | | 5 | 0 | 0.711111 | | | ± 0.654654 | 0.544444 | | | ± 1 | 0.100000 | | 6 | ± 0.285232 | 0.554858 | | | ± 0.765055 | 0.378475 | | | ± 1 | 0.0666667 |
The Abscissas and weights can be computed analytically for small 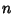 . . See also Chebyshev Quadrature, Radau Quadrature
References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 888-890, 1972.Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 465, 1987. Chandrasekhar, S. Radiative Transfer. New York: Dover, pp. 63-64, 1960. Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 343-345, 1956. |
![]() in which the endpoints of the interval
in which the endpoints of the interval ![]() are included in a total of
are included in a total of ![]() Abscissas, giving
Abscissas, giving ![]() freeabscissas. Abscissas are symmetrical about the origin, and the general Formula is
freeabscissas. Abscissas are symmetrical about the origin, and the general Formula is
![]() .
.