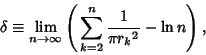| 释义 |
Masser-Gramain ConstantN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Let 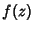 be an Entire Function such that be an Entire Function such that  is an Integer for each Positive Integer is an Integer for each Positive Integer 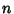 . Then Pólya (1915) showed that if . Then Pólya (1915) showed that if
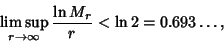 | (1) |
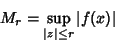 | (2) |
 is a Polynomial. Furthermore, is a Polynomial. Furthermore,  is the best constant (i.e., counterexamplesexist for every smaller value). is the best constant (i.e., counterexamplesexist for every smaller value).
If 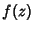 is an Entire Function with is an Entire Function with  a Gaussian Integer for each Gaussian Integer a Gaussian Integer for each Gaussian Integer 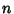 , thenGelfond (1929) proved that there exists a constant , thenGelfond (1929) proved that there exists a constant 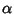 such that such that
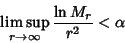 | (3) |
 is a Polynomial. Gramain (1981, 1982) showed that the best such constant is is a Polynomial. Gramain (1981, 1982) showed that the best such constant is
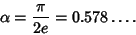 | (4) |
 must be a Polynomial if must be a Polynomial if
 | (5) |
 | (6) |
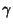 is the Euler-Mascheroni Constant, is the Euler-Mascheroni Constant, 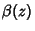 is the Dirichlet Beta Function, is the Dirichlet Beta Function,
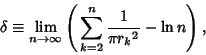 | (7) |
 is the minimum Nonnegative is the minimum Nonnegative 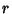 for which there exists a Complex Number for which there exists a Complex Number 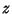 for which the ClosedDisk with center for which the ClosedDisk with center 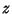 and radius and radius 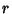 contains at least contains at least 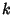 distinct Gaussian Integers. Gosper gave distinct Gaussian Integers. Gosper gave
 | (8) |
 | (9) |
 | (10) |
 | (11) |
 | (12) |
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/masser/masser.htmlGramain, F. ``Sur le théorème de Fukagawa-Gel'fond.'' Invent. Math. 63, 495-506, 1981. Gramain, F. ``Sur le théorème de Fukagawa-Gel'fond-Gruman-Masser.'' Séminaire Delange-Pisot-Poitou (Théorie des Nombres), 1980-1981. Boston, MA: Birkhäuser, 1982. Gramain, F. and Weber, M. ``Computing and Arithmetic Constant Related to the Ring of Gaussian Integers.'' Math. Comput. 44, 241-245, 1985. Gramain, F. and Weber, M. ``Computing and Arithmetic Constant Related to the Ring of Gaussian Integers.'' Math. Comput. 48, 854, 1987. Masser, D. W. ``Sur les fonctions entières à valeurs entières.'' C. R. Acad. Sci. Paris Sér. A-B 291, A1-A4, 1980.
|
![]() be an Entire Function such that
be an Entire Function such that ![]() is an Integer for each Positive Integer
is an Integer for each Positive Integer ![]() . Then Pólya (1915) showed that if
. Then Pólya (1915) showed that if![]() is an Entire Function with
is an Entire Function with ![]() a Gaussian Integer for each Gaussian Integer
a Gaussian Integer for each Gaussian Integer ![]() , thenGelfond (1929) proved that there exists a constant
, thenGelfond (1929) proved that there exists a constant ![]() such that
such that