| 释义 |
Modular EquationThe modular equation of degree 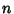 gives an algebraic connection of the form gives an algebraic connection of the form
 | (1) |
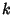 and and  . When . When 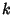 and and  satisfy a modular equation, arelationship of the form satisfy a modular equation, arelationship of the form
 | (2) |
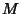 is called the Modular Function Multiplier. In general, if is called the Modular Function Multiplier. In general, if  is an Odd Prime, then themodular equation is given by is an Odd Prime, then themodular equation is given by
 | (3) |
 | (4) |
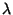 is a Elliptic Lambda Function, and is a Elliptic Lambda Function, and
 | (5) |
 | (6) |
 | (7) |
 | (8) |
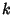 and and  areIn terms of areIn terms of  and and  , ,
 | (14) |
 | (15) |
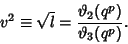 | (16) |
 are Theta Functions. are Theta Functions.
A modular equation of degree  for for  can be obtained by iterating the equation for can be obtained by iterating the equation for 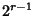 . Modular equationsfor Prime . Modular equationsfor Prime  from 3 to 23 are given in Borwein and Borwein (1987). from 3 to 23 are given in Borwein and Borwein (1987).
Quadratic modular identities include
 | (17) |
 | (18) |
 | (19) |
 | (20) |
 | (21) |
 | (22) |
 | (23) |
References
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 127-132, 1987.Hanna, M. ``The Modular Equations.'' Proc. London Math. Soc. 28, 46-52, 1928. Ramanujan, S. ``Modular Equations and Approximations to  .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914. .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
|
![]() gives an algebraic connection of the form
gives an algebraic connection of the form

![]() for
for ![]() can be obtained by iterating the equation for
can be obtained by iterating the equation for ![]() . Modular equationsfor Prime
. Modular equationsfor Prime ![]() from 3 to 23 are given in Borwein and Borwein (1987).
from 3 to 23 are given in Borwein and Borwein (1987).



![]() .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.