| 释义 |
Morgan-Voyce PolynomialPolynomials related to the Brahmagupta Polynomials. They are defined by theRecurrence Relations
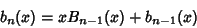 | (1) |
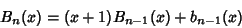 | (2) |
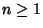 , with , with
 | (3) |
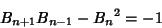 | (4) |
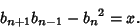 | (5) |
Defining the Matrix
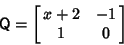 | (8) |
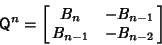 | (9) |
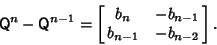 | (10) |
Defining
gives
and
The Morgan-Voyce polynomials are related to the Fibonacci Polynomials 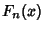 by by
(Swamy 1968).
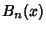 satisfies the Ordinary Differential Equation satisfies the Ordinary Differential Equation
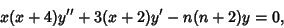 | (19) |
 the equation the equation
 | (20) |
References
Lahr, J. ``Fibonacci and Lucas Numbers and the Morgan-Voyce Polynomials in Ladder Networks and in Electric Line Theory.'' In Fibonacci Numbers and Their Applications (Ed. G. E. Bergum, A. N. Philippou, and A. F. Horadam). Dordrecht, Netherlands: Reidel, 1986.Morgan-Voyce, A. M. ``Ladder Network Analysis Using Fibonacci Numbers.'' IRE Trans. Circuit Th. CT-6, 321-322, Sep. 1959. Swamy, M. N. S. ``Properties of the Polynomials Defined by Morgan-Voyce.'' Fib. Quart. 4, 73-81, 1966. Swamy, M. N. S. ``More Fibonacci Identities.'' Fib. Quart. 4, 369-372, 1966. Swamy, M. N. S. ``Further Properties of Morgan-Voyce Polynomials.'' Fib. Quart. 6, 167-175, 1968.
|
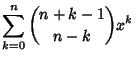

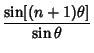

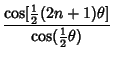
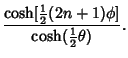
![]() by
by![]() satisfies the Ordinary Differential Equation
satisfies the Ordinary Differential Equation