| 释义 |
Natural LogarithmThe Logarithm having base e, where
 | (1) |
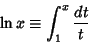 | (2) |
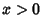 . The natural logarithm can also be defined for Complex Numbers as . The natural logarithm can also be defined for Complex Numbers as
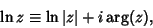 | (3) |
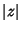 is the Modulus and is the Modulus and 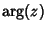 is the Argument. The natural logarithm is especially useful in Calculus because its Derivativeis given by the simple equation is the Argument. The natural logarithm is especially useful in Calculus because its Derivativeis given by the simple equation
 | (4) |
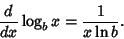 | (5) |
The Mercator Series
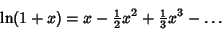 | (6) |
Continued Fraction representations of logarithmic functions include
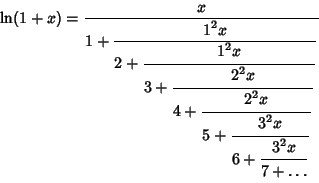 | (7) |
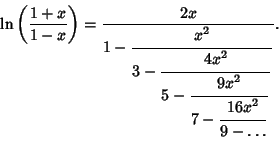 | (8) |
For a Complex Number  , the natural logarithm satisfies , the natural logarithm satisfies
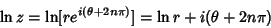 | (9) |
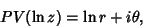 | (10) |
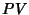 is the Principal Value. is the Principal Value.
Some special values of the natural logarithm are
 | (11) |
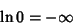 | (12) |
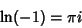 | (13) |
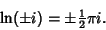 | (14) |
An identity for the natural logarithm of 2 discovered using the PSLQ Algorithm is
 | (15) |
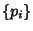 is given by the periodic sequence obtained by appending copies of is given by the periodic sequence obtained by appending copies of 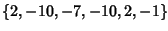 (in other words, (in other words,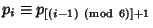 for for  ) (Bailey et al. 1995, Bailey and Plouffe).See also e, Jensen's Formula, Lg, Logarithm ) (Bailey et al. 1995, Bailey and Plouffe).See also e, Jensen's Formula, Lg, Logarithm
References
Bailey, D.; Borwein, P.; and Plouffe, S. ``On the Rapid Computation of Various Polylogarithmic Constants.'' http://www.cecm.sfu.ca/~pborwein/PAPERS/P123.ps.Bailey, D. and Plouffe, S. ``Recognizing Numerical Constants.'' http://www.cecm.sfu.ca/organics/papers/bailey/. |
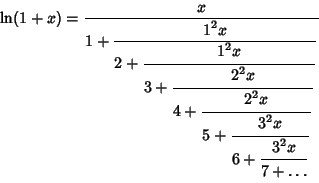
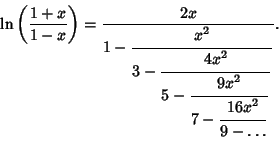
![]() , the natural logarithm satisfies
, the natural logarithm satisfies