| 释义 |
Polynomial Remainder TheoremIf the Coefficients of the Polynomial
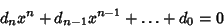 | (1) |
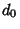 and a Denominator which is a factor of and a Denominator which is a factor of 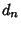 (with either sign possible). This follows since aPolynomial of Order (with either sign possible). This follows since aPolynomial of Order  with with  integral Roots can be expressed as integral Roots can be expressed as
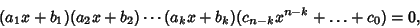 | (2) |
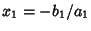 , , 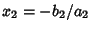 , ..., and , ..., and 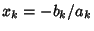 . Factoring out the . Factoring out the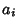 s, s,
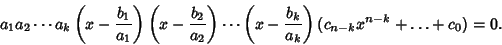 | (3) |
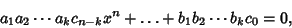 | (4) |
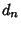 and and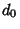 , all the integral roots of (1) are of the form [factors of , all the integral roots of (1) are of the form [factors of 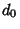 ]/[factors of ]/[factors of 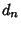 ]. ].
|