78 circumcircle

Chord theorems

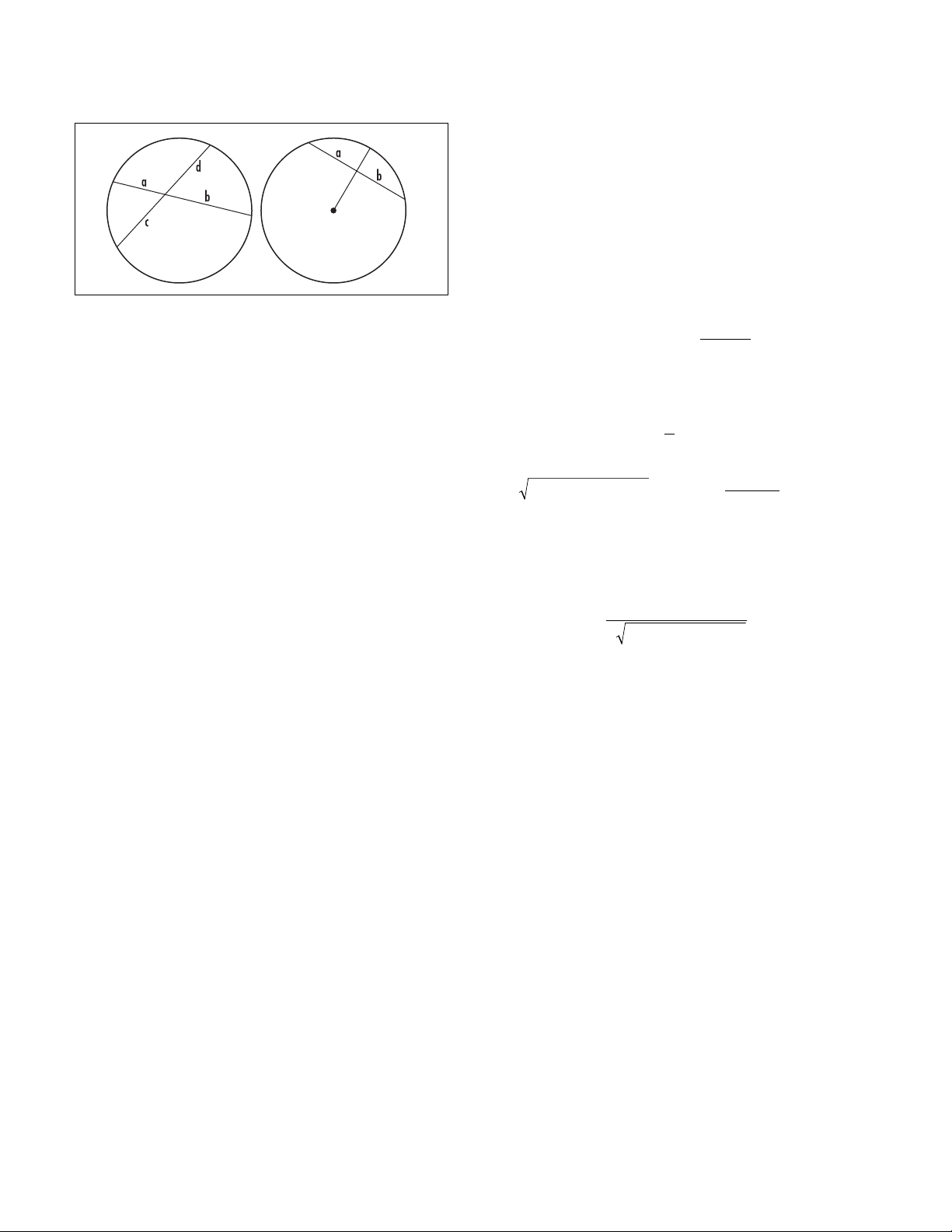
a

iii. Opposite angles in a cyclic

QUADRILATERAL

sum to 180°.

3. Two-Chord Theorem

In the diagram above, we have: ab = cd.

This is proved by connecting the endpoints of

the chords to create two triangles. The inscribed-

angle theorems show that these two triangles are

similar by the AAA rule. Consequently, a/c = d/b.

4. Radius-Chord Theorem

In the right-hand side of the diagram, we see that:

The radius of a circle bisects a chord (that

is, we have a= b) if, and only if, the radius

is perpendicular to the chord.

This is proved by drawing two radii to the endpoints

of the chord to produce a large isosceles triangle. If

the central radius is at 90°to the chord, this produces

two congruent right triangles, and so a= b. Con-

versely, if we are told a= b, then the

LAW OF COSINES

,

applied to each base angle of the isosceles triangle,

shows that the central radius intercepts the chord at

an angle of 90°.

See also

AAA

/

AAS

/

ASA

/

SAS

/

SSS

;

CONGRUENT FIGURES

;

CYCLIC POLYGON

; P

TOLEMY

’

S THEOREM

;

SECANT

;

SIMI

-

LAR FIGURES

.

circumcircle A circle that passes through all three ver-

tices of the triangle is called a circumcircle for the trian-

gle. That three distinct points in the plane determine a

unique circle was first proved by E

UCLID

in his treatise,

T

HE

E

LEMENTS

,Book III. Euclid also presented a gen-

eral method for actually constructing the circumcircle of

a triangle. (This result was later generalized by A

POLLO

-

NIUS OF

P

ERGA

, who showed how to construct a circle

tangent to any three points, lines, or circles in the plane.)

The center of the circumcircle of a triangle is called

its circumcenter. Clearly, it is a point

EQUIDISTANT

from

the three vertices, and so it must lie on each line of

points equidistant from any two vertices. The circum-

center of a triangle can thus be found by drawing the

perpendicular bisectors of the sides of the triangle and

locating where these three lines meet.

By the

LAW OF SINES

, the radius of the circumcircle

of a triangle is given by , where a is

a side-length of the triangle and Ais the angle opposite

that chosen side. If the remaining two sides of the trian-

gle have lengths band c, then the area of the triangle

can be written: . By

HERON

’

S

FORMULA

, this area can also be computed via

where . Equating

these two equations, solving for sin(A),and substitut-

ing into the formula above produces a formula for the

radius of the circumcircle of a triangle solely in terms

of its side lengths:

The circumcircle of a regular

POLYGON

is that cir-

cle that passes through all the vertices of the polygon.

The radius of the circumcircle of a square, for example,

of side-length xis r= x/√

–

2.

See also

CONCURRENT

;

LONG RADIUS

;

TRIANGLE

.

circumscribe/inscribe If Aand Bare two geometric

figures, with Ainside B, drawn so that the two figures

have points in common but do not have edges that

cross, then we say that figure Ais inscribed in B, or,

alternatively, that figure Bis circumscribed about A.

For example, a polygon lying inside a circle with all its

vertices on that circle is said to be inscribed in the cir-

cle, and a circle inside a polygon touching each side of

the polygon is inscribed in the polygon. A circle that

passes through all three vertices of a triangle circum-

scribes that triangle, and the smallest square that sur-

rounds a circle circumscribes that circle.

See also

CIRCUMCIRCLE

;

INCIRCLE

.

clock math See

MODULAR ARITHMETIC

.