The Greek scholars of antiquity were the first to
study conic sections. With no practical applications in
mind, mathematicians pursued the topic solely for its
beauty and its intellectual rewards. Around 225
B
.
C
.
E
.
A
POLLONIUS OF
P
ERGA
wrote a series of eight books,
titled The Conics, in which he thoroughly investigated
these curves. He introduced the names parabola,
ellipse, and hyperbola. A
RCHIMEDES OF
S
YRACUSE
(ca.
287–212
B
.
C
.
E
.) also wrote about these curves. Almost
2,000 years later, scientists began finding applications
of conic sections to problems in the real world. In 1604
G
ALILEO
G
ALILEI
discovered that objects thrown in the
air follow parabolic paths (if air resistance can be
neglected), and in 1609 astronomer J
OHANNES
K
EPLER
discovered that the orbit of Mars is an ellipse. He con-
jectured that all planetary bodies have elliptical orbits,
which, 60 years later, I
SAAC NEWTON
was able to prove
using his newly developed law of gravitation. This cen-
tury, scientists have discovered that the path of an
alpha particle in the electrical field of an atomic
nucleus is a hyperbola.
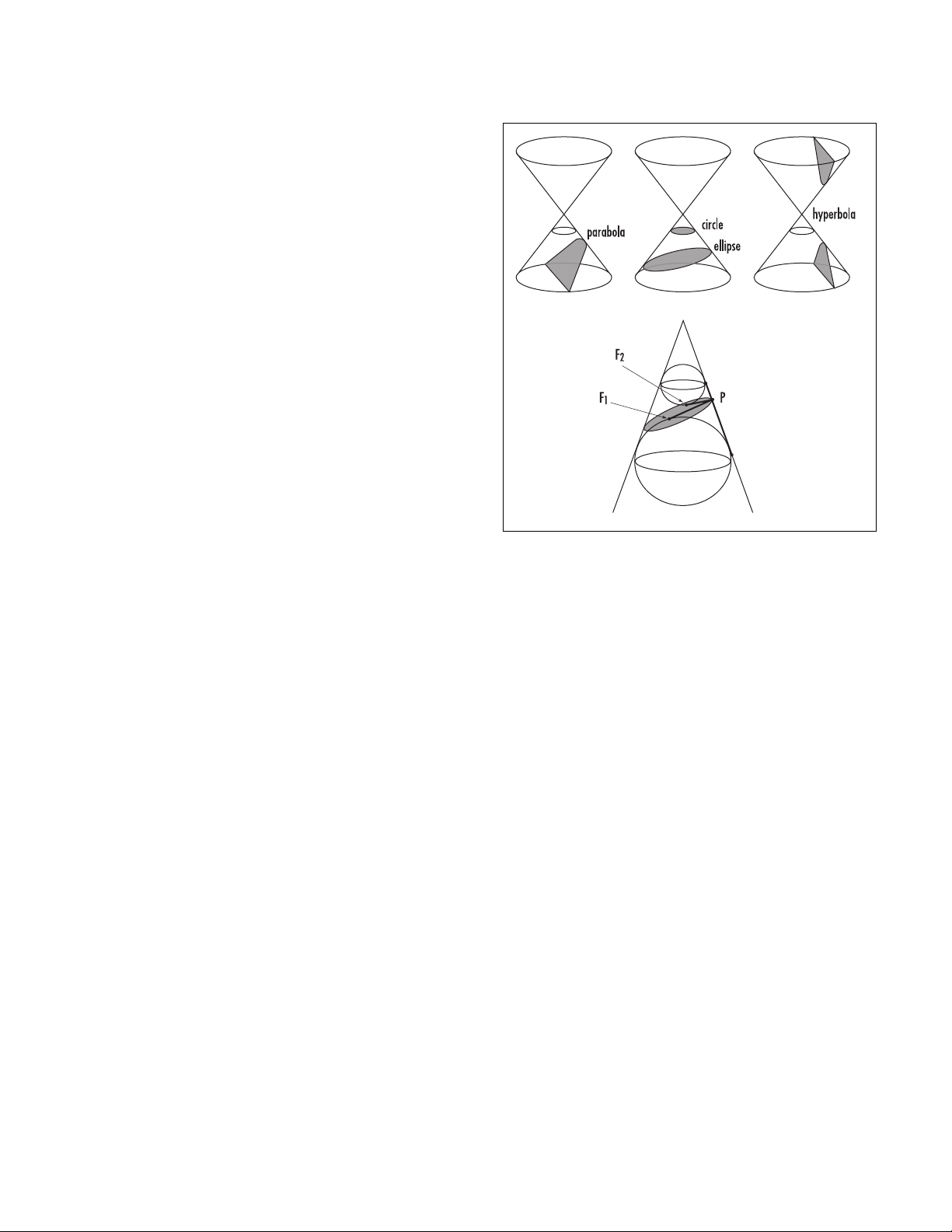
The conic sections can be described solely by prop-
erties they possess as curves in a plane. We see this by
drawing spheres internally tangent to the cone and tan-
gent to the slicing plane defining the curve. For exam-
ple, given an ellipse, if two internal spheres are tangent
to the plane at points F1and F2, then for any point P
on the ellipse, its distance from F1is the same as its dis-
tance from the circle of tangency of the lower sphere,
and its distance from F2is the same as its distance from
the circle of tangency of the upper sphere. Conse-
quently, the sum of its distances from F1and F2equals
the fixed distance between the two spheres as measured
along the side of the cone. This property can be used to
define an ellipse:
An ellipse is the set of all points in the plane
whose distances from two given points, F1and
F2, have a constant sum.
By drawing spheres, one in each nappe of the cone and
tangent to the slicing plane of a hyperbola, one can
show in an analogous way:
A hyperbola is the set of all points in the plane
whose distances from two given points, F1and
F2, have a constant difference.
For a parabola, one draws a single sphere tangent to
the slicing plane of the parabola and considers the
point Fat which the sphere touches the plane, and the
line Lof intersection of the slicing plane with the plane
of the circle along which the sphere is tangent to the
cone. We have:
A parabola is the set of all points in the plane
the same distance from a point Fin the plane
and a given line L.
The conic sections have remarkable reflection properties.
See also
PROJECTION
.
conjunction (“and” statement) In
FORMAL LOGIC
a
compound statement of the form “pand q” is known
as a conjunction. For example, “A triangle has three
sides and a square has four sides” is a conjunction. A
conjunction is denoted in symbols by pq.
For a conjunction as a whole to be considered true,
each component (or conjunct) pand qmust itself be
true. Thus a conjunction has the following
TRUTH TABLE
:
∨
conjunction 93
The conic sections