Simpson's rule
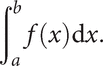
Divide [a, b] into n equal subintervals of length h by the partition
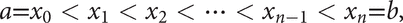
where xi+1−xi = h=(b−a)/n, where n is even. Denote f(xi) by fi, and let Pi be the point (xi, fi). Take an arc of the parabola through the points P0, P1, and P2, an arc of a parabola through P2, P3, and P4, similarly, and so on. This is why n is necessarily even. The resulting Simpson's rule gives
as an approximation to the integral. In general, Simpson's rule is much more accurate than the trapezium rule, and the error is bounded by
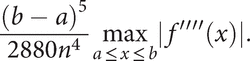
The rule is named after the English mathematician Thomas Simpson (1710–61), though the rule is due to Newton, as Simpson himself acknowledged.
- centre of symmetry
- centrifugal force
- centripetal force
- centroid
- centroid
- Cesàro summation
- Ceva's Theorem
- chain rule
- chain rule
- Chalkdust
- chance nodes
- chance variable
- change of base
- change of basis
- change of coordinates
- change of observer
- change of variable
- chaos
- character
- characteristic
- characteristic equation
- characteristic function
- characteristic function
- characteristic of a field
- characteristic polynomial